Metamath
Download worked project
Metamath is a language that can express theorems, accompanied by proofs that can be verified by a computer program. Its website lets you browse from complex theorems up to the most basic axioms they rely on to be proven.
The purpose of this project is to visualize the steps of the proof as a graph, and visualize statement frequencies.
DISCLAIMER: No panic !
You DO NOT need to understand any of the mathematics which follows. Here we are only interested in parsing the data and visualize it
REQUIREMENTS: Having read Relational data tutorial , which contains also instructions for installing required libraries.
What to do
Unzip exercises zip in a folder, you should obtain something like this:
metamath-prj
metamath.ipynb
metamath-sol.ipynb
db.mm
proof.txt
soft.py
jupman.py
WARNING: to correctly visualize the notebook, it MUST be in an unzipped folder !
open Jupyter Notebook from that folder. Two things should open, first a console and then a browser. The browser should show a file list: navigate the list and open the notebook
metamath.ipynbGo on reading the notebook, and write in the appropriate cells when asked
Shortcut keys:
to execute Python code inside a Jupyter cell, press
Control + Enterto execute Python code inside a Jupyter cell AND select next cell, press
Shift + Enterto execute Python code inside a Jupyter cell AND a create a new cell aftwerwards, press
Alt + EnterIf the notebooks look stuck, try to select
Kernel -> Restart
Metamath db
For this exercise, we have two files to consider:
db.mm contains the description of a simple algebra where you can only add zero to variables
proof.txt contains the awesome proof that… any variable is equal to itself
First you will load db.mm and parse text file into Python, here is the full content:
$( Declare the constant symbols we will use $)
$c 0 + = -> ( ) term wff |- $.
$( Declare the metavariables we will use $)
$v t r s P Q $.
$( Specify properties of the metavariables $)
tt $f term t $.
tr $f term r $.
ts $f term s $.
wp $f wff P $.
wq $f wff Q $.
$( Define "term" and "wff" $)
tze $a term 0 $.
tpl $a term ( t + r ) $.
weq $a wff t = r $.
wim $a wff ( P -> Q ) $.
$( State the axioms $)
a1 $a |- ( t = r -> ( t = s -> r = s ) ) $.
a2 $a |- ( t + 0 ) = t $.
$( Define the modus ponens inference rule $)
${
min $e |- P $.
maj $e |- ( P -> Q ) $.
mp $a |- Q $.
$}
Format description:
Each row is a statement
Words are separated by spaces. Each word that appears in a statement is called a token
Tokens starting with dollar
$are called keywords, you may have$(,$),$c,$v,$a,$f,${,$},$.Statements may be identified with a unique arbitrary label, which is placed at the beginning of the row. For example,
tt,weq,majare all labels (in the file there are more):tt $f term t $.weq $a wff t = r $.maj $e |- ( P -> Q ) $.
Some rows have no label, examples:
$c 0 + = -> ( ) term wff |- $.$v t r s P Q $.$( State the axioms $)${$}
in each row, after the first dollar keyword, you may have an arbitratry sequence of characters terminated by a dollar followed by a dot
$.. You don’t need to care about the sequence meaning! Examples:tt $f term t $.has sequenceterm tweq $a wff t = r $.has sequencewff t = r$v t r s P Q $.has sequencet r s P Q
Now implement function parse_db which scans the file line by line (it is a text file, so you can use line files examples), parses ONLY rows with labels, and RETURN a dictionary mapping labels to remaining data in the row represented as a dictionary, formatted like this (showing here only first three labels):
{'a1': {'keyword': '$a',
'sequence': '|- ( t = r -> ( t = s -> r = s ) )'},
'a2': {'keyword': '$a',
'sequence': '|- ( t + 0 ) = t'},
'maj': {'keyword': '$e',
'sequence': '|- ( P -> Q )'},
'min': {'keyword': '$e', 'sequence': '|- P'},
'mp': {'keyword': '$a', 'sequence': '|- Q'},
'tpl': {'keyword': '$a', 'sequence': 'term ( t + r )'},
'tr': {'keyword': '$f', 'sequence': 'term r'},
'ts': {'keyword': '$f', 'sequence': 'term s'},
'tt': {'keyword': '$f', 'sequence': 'term t'},
'tze': {'keyword': '$a', 'sequence': 'term 0'},
'weq': {'keyword': '$a', 'sequence': 'wff t = r'},
'wim': {'keyword': '$a', 'sequence': 'wff ( P -> Q )'},
'wp': {'keyword': '$f', 'sequence': 'wff P'},
'wq': {'keyword': '$f', 'sequence': 'wff Q'}
}
1. Metamath db
Show solution[3]:
def parse_db(filepath):
raise Exception('TODO IMPLEMENT ME !')
db_mm = parse_db('db.mm')
assert db_mm['tt'] == {'keyword': '$f', 'sequence': 'term t'}
assert db_mm['maj'] == {'keyword': '$e', 'sequence': '|- ( P -> Q )'}
# careful 'mp' label shouldn't have spaces inside !
assert 'mp' in db_mm
assert db_mm['mp'] == {'keyword': '$a', 'sequence': '|- Q'}
from pprint import pprint
pprint(db_mm)
2.1 Metamath proof
A proof file is made of steps, one per row. Each statement, in order to be proven, needs other steps to be proven until very basic facts called axioms are reached, which need no further proof (typically proofs in Metamath are shown in much shorter format, but here we use a more explicit way)
So a proof can be nicely displayed as a tree of the steps it is made of, where the top node is the step to be proven and the axioms are the leaves of the tree.
Complete content of proof.txt:
1 tt $f term t
2 tze $a term 0
3 1,2 tpl $a term ( t + 0 )
4 tt $f term t
5 3,4 weq $a wff ( t + 0 ) = t
6 tt $f term t
7 tt $f term t
8 6,7 weq $a wff t = t
9 tt $f term t
10 9 a2 $a |- ( t + 0 ) = t
11 tt $f term t
12 tze $a term 0
13 11,12 tpl $a term ( t + 0 )
14 tt $f term t
15 13,14 weq $a wff ( t + 0 ) = t
16 tt $f term t
17 tze $a term 0
18 16,17 tpl $a term ( t + 0 )
19 tt $f term t
20 18,19 weq $a wff ( t + 0 ) = t
21 tt $f term t
22 tt $f term t
23 21,22 weq $a wff t = t
24 20,23 wim $a wff ( ( t + 0 ) = t -> t = t )
25 tt $f term t
26 25 a2 $a |- ( t + 0 ) = t
27 tt $f term t
28 tze $a term 0
29 27,28 tpl $a term ( t + 0 )
30 tt $f term t
31 tt $f term t
32 29,30,31 a1 $a |- ( ( t + 0 ) = t -> ( ( t + 0 ) = t -> t = t ) )
33 15,24,26,32 mp $a |- ( ( t + 0 ) = t -> t = t )
34 5,8,10,33 mp $a |- t = t
Each line represents a step of the proof. Last line is the final goal of the proof.
Each line contains, in order:
a step number at the beginning, starting from 1 (
step_id)possibly a list of other step_ids, separated by commas, like
29,30,31- they are references to previous rowslabel of the
db_mmstatement referenced by the step, likett,tze,weq- that label must have been defined somewhere indb.mmfilestatement type: a token starting with a dollar, like
$a,$fa sequence of characters, like (for you they are just characters, don’t care about the meaning !):
term ( t + 0 )|- ( ( t + 0 ) = t -> ( ( t + 0 ) = t -> t = t ) )
Implement function parse_proof, which takes a filepath to the proof and RETURN a list of steps expressed as a dictionary, in this format (showing here only first 5 items):
NOTE: referenced step_ids are integer numbers and they are the original ones from the file, meaning they start from one.
[
{'keyword': '$f',
'label': 'tt',
'sequence': 'term t',
'step_ids': []},
{'keyword': '$a',
'label': 'tze',
'sequence': 'term 0',
'step_ids': []},
{'keyword': '$a',
'label': 'tpl',
'sequence': 'term ( t + 0 )',
'step_ids': [1,2]},
{'keyword': '$f',
'label': 'tt',
'sequence': 'term t',
'step_ids': []},
{'keyword': '$a',
'label': 'weq',
'sequence': 'wff ( t + 0 ) = t',
'step_ids': [3,4]},
.
.
.
]
[5]:
def parse_proof(filepath):
raise Exception('TODO IMPLEMENT ME !')
proof = parse_proof('proof.txt')
assert proof[0] == {'keyword': '$f', 'label': 'tt', 'sequence': 'term t', 'step_ids': []}
assert proof[1] == {'keyword': '$a', 'label': 'tze', 'sequence': 'term 0', 'step_ids': []}
assert proof[2] == {'keyword': '$a',
'label': 'tpl',
'sequence': 'term ( t + 0 )',
'step_ids': [1, 2]}
assert proof[4] == {'keyword': '$a',
'label': 'weq',
'sequence': 'wff ( t + 0 ) = t',
'step_ids': [3,4]}
assert proof[33] == { 'keyword': '$a',
'label': 'mp',
'sequence': '|- t = t',
'step_ids': [5, 8, 10, 33]}
pprint(proof)
[{'keyword': '$f', 'label': 'tt', 'sequence': 'term t', 'step_ids': []},
{'keyword': '$a', 'label': 'tze', 'sequence': 'term 0', 'step_ids': []},
{'keyword': '$a',
'label': 'tpl',
'sequence': 'term ( t + 0 )',
'step_ids': [1, 2]},
{'keyword': '$f', 'label': 'tt', 'sequence': 'term t', 'step_ids': []},
{'keyword': '$a',
'label': 'weq',
'sequence': 'wff ( t + 0 ) = t',
'step_ids': [3, 4]},
{'keyword': '$f', 'label': 'tt', 'sequence': 'term t', 'step_ids': []},
{'keyword': '$f', 'label': 'tt', 'sequence': 'term t', 'step_ids': []},
{'keyword': '$a', 'label': 'weq', 'sequence': 'wff t = t', 'step_ids': [6, 7]},
{'keyword': '$f', 'label': 'tt', 'sequence': 'term t', 'step_ids': []},
{'keyword': '$a',
'label': 'a2',
'sequence': '|- ( t + 0 ) = t',
'step_ids': [9]},
{'keyword': '$f', 'label': 'tt', 'sequence': 'term t', 'step_ids': []},
{'keyword': '$a', 'label': 'tze', 'sequence': 'term 0', 'step_ids': []},
{'keyword': '$a',
'label': 'tpl',
'sequence': 'term ( t + 0 )',
'step_ids': [11, 12]},
{'keyword': '$f', 'label': 'tt', 'sequence': 'term t', 'step_ids': []},
{'keyword': '$a',
'label': 'weq',
'sequence': 'wff ( t + 0 ) = t',
'step_ids': [13, 14]},
{'keyword': '$f', 'label': 'tt', 'sequence': 'term t', 'step_ids': []},
{'keyword': '$a', 'label': 'tze', 'sequence': 'term 0', 'step_ids': []},
{'keyword': '$a',
'label': 'tpl',
'sequence': 'term ( t + 0 )',
'step_ids': [16, 17]},
{'keyword': '$f', 'label': 'tt', 'sequence': 'term t', 'step_ids': []},
{'keyword': '$a',
'label': 'weq',
'sequence': 'wff ( t + 0 ) = t',
'step_ids': [18, 19]},
{'keyword': '$f', 'label': 'tt', 'sequence': 'term t', 'step_ids': []},
{'keyword': '$f', 'label': 'tt', 'sequence': 'term t', 'step_ids': []},
{'keyword': '$a',
'label': 'weq',
'sequence': 'wff t = t',
'step_ids': [21, 22]},
{'keyword': '$a',
'label': 'wim',
'sequence': 'wff ( ( t + 0 ) = t -> t = t )',
'step_ids': [20, 23]},
{'keyword': '$f', 'label': 'tt', 'sequence': 'term t', 'step_ids': []},
{'keyword': '$a',
'label': 'a2',
'sequence': '|- ( t + 0 ) = t',
'step_ids': [25]},
{'keyword': '$f', 'label': 'tt', 'sequence': 'term t', 'step_ids': []},
{'keyword': '$a', 'label': 'tze', 'sequence': 'term 0', 'step_ids': []},
{'keyword': '$a',
'label': 'tpl',
'sequence': 'term ( t + 0 )',
'step_ids': [27, 28]},
{'keyword': '$f', 'label': 'tt', 'sequence': 'term t', 'step_ids': []},
{'keyword': '$f', 'label': 'tt', 'sequence': 'term t', 'step_ids': []},
{'keyword': '$a',
'label': 'a1',
'sequence': '|- ( ( t + 0 ) = t -> ( ( t + 0 ) = t -> t = t ) )',
'step_ids': [29, 30, 31]},
{'keyword': '$a',
'label': 'mp',
'sequence': '|- ( ( t + 0 ) = t -> t = t )',
'step_ids': [15, 24, 26, 32]},
{'keyword': '$a',
'label': 'mp',
'sequence': '|- t = t',
'step_ids': [5, 8, 10, 33]}]
2. Checking proof
If you’ve done everything properly, by executing following cells you should be be able to see nice graphs.
IMPORTANT: You do not need to implement anything!
Just look if results match expected graphs
Overview plot
Here we only show step numbers using function draw_proof defined in sciprog library
[6]:
from soft import draw_proof
# uncomment and check
#draw_proof(proof, db_mm, only_ids=True) # all graph, only numbers
[7]:
print()
print('************************ EXPECTED COMPLETE GRAPH **********************************')
draw_proof(proof, db_mm, only_ids=True)
************************ EXPECTED COMPLETE GRAPH **********************************
Detail plot
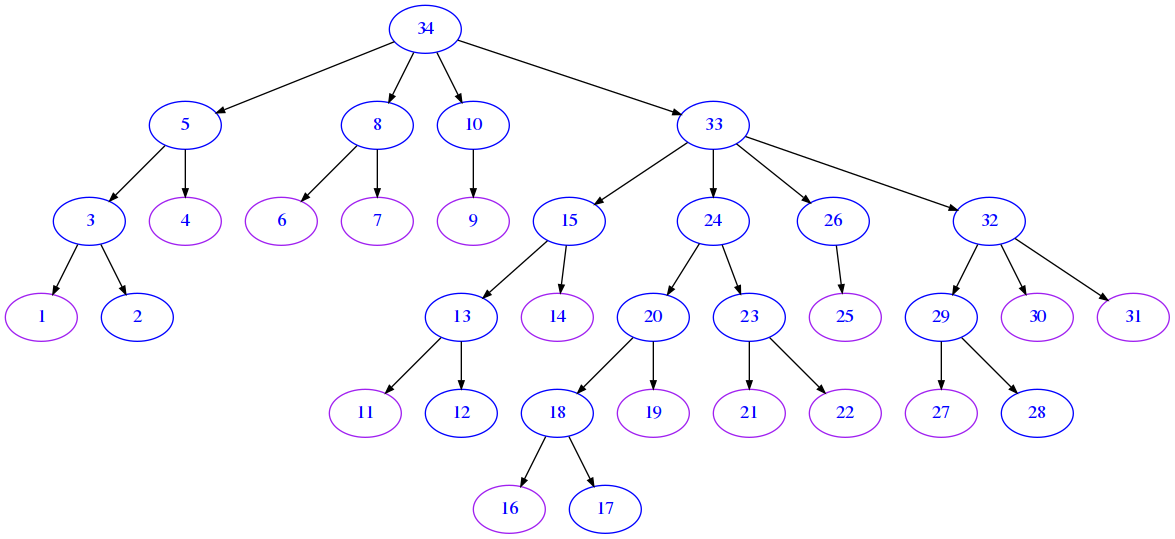
Here we show data from both the proof and the db_mm we calculated earlier. To avoid having a huge graph we only focus on subtree starting from step_id 24.
To understand what is shown, look at node 20: - first line contains statement wff ( t + 0 ) = t taken from line 20 of proof file - second line weq: wff t = r is taken from db_mm, and means rule labeled weq was used to derive the statement in the first line.
[8]:
# uncomment and check
#draw_proof(proof, db_mm, step_id=24)
[9]:
print()
print('************************* EXPECTED DETAIL GRAPH *******************************')
draw_proof(proof, db_mm, step_id=24)
************************* EXPECTED DETAIL GRAPH *******************************

3. Top statements
We can measure the importance of theorems and definitions (in general, statements) by counting how many times they are referenced in proofs.
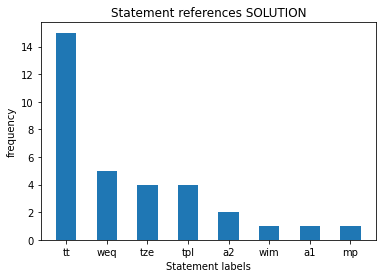
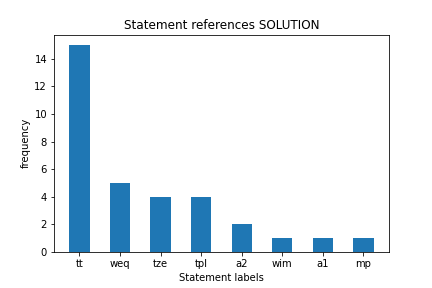
3.1 plot: Write some code to plot the histogram of statement labels referenced by steps in proof, from most to least frequently referenced.
A label gets a count each time a step references another step with that label.
For example, in the subgraph above:
ttis referenced 4 times, that is, there are 4 steps referencing other steps which contain the labelttweqis referenced 2 timestplandtzeare referenced 1 time eachwimis referenced 0 times (it is only present in the last node, which being the root node cannot be referenced by any step)
NOTE: the previous counts are just for the subgraph example.
In your exercise, you will need to consider all the steps
3.2 print list: Below the graph, print the list of labels from most to least frequent, associating them to corresponding statement sequence taken from db_mm
Expected output:
tt : term t
weq : wff t = r
tze : term 0
tpl : term ( t + r )
a2 : |- ( t + 0 ) = t
wim : wff ( P -> Q )
a1 : |- ( t = r -> ( t = s -> r = s ) )
mp : |- Q
[10]:
import numpy as np
import matplotlib.pyplot as plt
# write here
[ ]: