Relational data 2 - binary relations
Download exercises zip
We can use graphs to model relations of many kinds, like isCloseTo, isFriendOf, loves, etc. Here we review some of them and their properties.
Before going on, make sure to have read the first tutorial Relational data
What to do
unzip exercises in a folder, you should get something like this:
relational
relational1-intro.ipynb
relational1-intro-sol.ipynb
relational2-binrel.ipynb
relational2-binrel-sol.ipynb
relational3-simple-stats.ipynb
relational3-simple-stats-sol.ipynb
relational4-chal.ipynb
jupman.py
soft.py
WARNING: to correctly visualize the notebook, it MUST be in an unzipped folder !
open Jupyter Notebook from that folder. Two things should open, first a console and then browser. The browser should show a file list: navigate the list and open the notebook
relational/relational2-binrel.ipynb
WARNING 2: DO NOT use the Upload button in Jupyter, instead navigate in Jupyter browser to the unzipped folder !
Go on reading that notebook, and follow instuctions inside.
Shortcut keys:
to execute Python code inside a Jupyter cell, press
Control + Enterto execute Python code inside a Jupyter cell AND select next cell, press
Shift + Enterto execute Python code inside a Jupyter cell AND a create a new cell aftwerwards, press
Alt + EnterIf the notebooks look stuck, try to select
Kernel -> Restart
Reflexive relations
A graph is reflexive when each node links to itself.
In real life, the typical reflexive relation could be “is close to” , supposing “close to” means being within a 100 meters distance. Obviously, any place is always close to itself, let’s see an example (Povo is a small town around Trento):
[2]:
from soft import draw_adj
draw_adj({
'Trento Cathedral' : ['Trento Cathedral', 'Trento Neptune Statue'],
'Trento Neptune Statue' : ['Trento Neptune Statue', 'Trento Cathedral'],
'Povo' : ['Povo'],
})

Some relations might not always be necessarily reflexive, like “did homeworks for”. You should always do your own homeworks, but to our dismay, university intelligence services caught some of you cheating. In the following example we expose the situation - due to privacy concerns, we identify students with numbers starting from zero included:
[3]:
from soft import draw_mat
draw_mat(
[
[True, False, False, False],
[False, False, False, False],
[False, True, True, False],
[False, False, False, False],
]
)
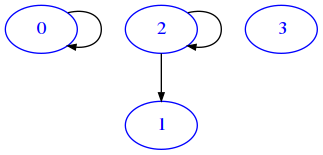
From the graph above, we see student 0 and student 2 both did their own homeworks. Student 3 did no homerworks at all. Alarmingly, we notice student 2 did the homeworks for student 1. Resulting conspiration shall be severely punished with a one year ban from having spritz at Emma’s bar.
Exercise - is_reflexive_mat
✪✪ Implement a function that RETURN True if \(n\) x \(n\) boolean matrix mat as list of lists is reflexive, False otherwise.
A graph is reflexive when all nodes point to themselves.
Please at least try to make the function efficient
[4]:
def is_reflexive_mat(mat):
raise Exception('TODO IMPLEMENT ME !')
assert is_reflexive_mat([ [False] ]) == False # m1
assert is_reflexive_mat([ [True] ]) == True # m2
assert is_reflexive_mat([ [False, False],
[False, False] ]) == False # m3
assert is_reflexive_mat([ [True, True],
[True, True] ]) == True # m4
assert is_reflexive_mat([ [True, True],
[False, True] ]) == True # m5
assert is_reflexive_mat([ [True, False],
[True, True] ]) == True # m6
assert is_reflexive_mat([ [True, True],
[True, False] ]) == False # m7
assert is_reflexive_mat([ [False, True],
[True, True] ]) == False # m8
assert is_reflexive_mat([ [False, True],
[True, False] ]) == False # m9
assert is_reflexive_mat([ [False, False],
[True, False] ]) == False # m10
assert is_reflexive_mat([ [False, True, True],
[True, False, False],
[True, True, True] ]) == False # m11
assert is_reflexive_mat([ [True, True, True],
[True, True, True],
[True, True, True] ]) == True # m12
Exercise - is_reflexive_adj
✪✪ Implement now the same function for dictionaries of adjacency lists:
RETURN True if provided graph as dictionary of adjacency lists is reflexive, False otherwise.
A graph is reflexive when all nodes point to themselves.
Please at least try to make the function efficient.
[5]:
def is_reflexive_adj(d):
raise Exception('TODO IMPLEMENT ME !')
assert is_reflexive_adj({ 'a':[] }) == False # d1
assert is_reflexive_adj({ 'a':['a'] }) == True # d2
assert is_reflexive_adj({ 'a':[],
'b':[]
}) == False # d3
assert is_reflexive_adj({ 'a':['a'],
'b':['b']
}) == True # d4
assert is_reflexive_adj({ 'a':['a','b'],
'b':['b']
}) == True # d5
assert is_reflexive_adj({ 'a':['a'],
'b':['a','b']
}) == True # d6
assert is_reflexive_adj({ 'a':['a','b'],
'b':['a']
}) == False # d7
assert is_reflexive_adj({ 'a':['b'],
'b':['a','b']
}) == False # d8
assert is_reflexive_adj({ 'a':['b'],
'b':['a']
}) == False # d9
assert is_reflexive_adj({ 'a':[],
'b':['a']
}) == False # d10
assert is_reflexive_adj({ 'a':['b','c'],
'b':['a'],
'c':['a','b','c']
}) == False # d11
assert is_reflexive_adj({ 'a':['a','b','c'],
'b':['a','b','c'],
'c':['a','b','c']
}) == True # d12
Symmetric relations
A graph is symmetric when for all nodes, if a node A links to another node B, there is a also a link from node B to A.
In real life, the typical symmetric relation is “is friend of”. If you are friend to somene, that someone should be also be your friend.
For example, since Scrooge typically is not so friendly with his lazy nephew Donald Duck, but certainly both Scrooge and Donald Duck enjoy visiting the farm of Grandma Duck, we can model their friendship relation like this:
[6]:
from soft import draw_adj
draw_adj({
'Donald Duck' : ['Grandma Duck'],
'Scrooge' : ['Grandma Duck'],
'Grandma Duck' : ['Scrooge', 'Donald Duck'],
})

Not that Scrooge is not linked to Donald Duck, but this does not mean the whole graph cannot be considered symmetric. If you pay attention to the definition above, there is if written at the beginning: if a node A links to another node B, there is a also a link from node B to A.
QUESTION: Looking purely at the above definition (so do not consider ‘is friend of’ relation), should a symmetric relation be necessarily reflexive?
Show answerQUESTION: Think about the semantics of the specific “is friend of” relation: can you think of a social network where the relation is not shown as reflexive?
Show answerQUESTION: Always talking about the specific semantics of “is friend of” relation: can you think about some case where it should be meaningful to store information about individuals not being friends of themselves ?
Show answerSome relations sometimes may or not be symmetric, depending on the graph at hand. Think about the relation loves. It is well known that Mickey Mouse loves Minnie and the sentiment is reciprocal, and Donald Duck loves Daisy Duck and the sentiment is reciprocal. We can conclude this particular graph is symmetrical:
[7]:
from soft import draw_adj
draw_adj({
'Donald Duck' : ['Daisy Duck'],
'Daisy Duck' : ['Donald Duck'],
'Mickey Mouse' : ['Minnie'],
'Minnie' : ['Mickey Mouse']
})
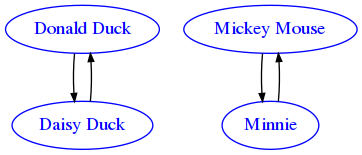
But what about this one? Donald Duck is not the only duck in town and sometimes a contender shows up: Gladstone Gander (Gastone in Italian) also would like the attention of Daisy ( never mind in some comics he actually gets it when Donald Duck messes up big time):
[8]:
from soft import draw_adj
draw_adj({
'Donald Duck' : ['Daisy Duck'],
'Daisy Duck' : ['Donald Duck'],
'Mickey Mouse' : ['Minnie'],
'Minnie' : ['Mickey Mouse'],
'Gladstone Gander' : ['Daisy Duck']
})

Exercise - is_symmetric_mat
✪✪ Implement an automated procedure to check whether or not a graph is symmetrical, which given a matrix as a list of lists that RETURN True if nxn boolean matrix mat as list of lists is symmetric, False otherwise.
A graph is symmetric when for all nodes, if a node A links to another node B, there is a also a link from node B to A.
[9]:
def is_symmetric_mat(mat):
raise Exception('TODO IMPLEMENT ME !')
assert is_symmetric_mat([ [False] ]) == True # m1
assert is_symmetric_mat([ [True] ]) == True # m2
assert is_symmetric_mat([ [False, False],
[False, False] ]) == True # m3
assert is_symmetric_mat([ [True, True],
[True, True] ]) == True # m4
assert is_symmetric_mat([ [True, True],
[False, True] ]) == False # m5
assert is_symmetric_mat([ [True, False],
[True, True] ]) == False # m6
assert is_symmetric_mat([ [True, True],
[True, False] ]) == True # m7
assert is_symmetric_mat([ [False, True],
[True, True] ]) == True # m8
assert is_symmetric_mat([ [False, True],
[True, False] ]) == True # m9
assert is_symmetric_mat([ [False, False],
[True, False] ]) == False # m10
assert is_symmetric_mat([ [False, True, True],
[True, False, False],
[True, True, True] ]) == False # m11
assert is_symmetric_mat([ [False, True, True],
[True, False, True],
[True, True, True] ]) == True # m12
Exercise - is_symmetric_adj
✪✪ Now implement the same as before but for a dictionary of adjacency lists:
RETURN True if given dictionary of adjacency lists is symmetric, False otherwise.
Assume all the nodes are represented in the keys.
A graph is symmetric when for all nodes, if a node A links to another node B, there is a also a link from node B to A.
[10]:
def is_symmetric_adj(d):
raise Exception('TODO IMPLEMENT ME !')
assert is_symmetric_adj({ 'a':[] }) == True # d1
assert is_symmetric_adj({ 'a':['a'] }) == True # d2
assert is_symmetric_adj({ 'a' : [],
'b' : []
}) == True # d3
assert is_symmetric_adj({ 'a' : ['a','b'],
'b' : ['a','b']
}) == True # d4
assert is_symmetric_adj({ 'a' : ['a','b'],
'b' : ['b']
}) == False # d5
assert is_symmetric_adj({ 'a' : ['a'],
'b' : ['a','b']
}) == False # d6
assert is_symmetric_adj({ 'a' : ['a','b'],
'b' : ['a']
}) == True # d7
assert is_symmetric_adj({ 'a' : ['b'],
'b' : ['a','b']
}) == True # d8
assert is_symmetric_adj({ 'a' : ['b'],
'b' : ['a']
}) == True # d9
assert is_symmetric_adj({ 'a' : [],
'b' : ['a']
}) == False # d10
assert is_symmetric_adj({ 'a' : ['b', 'c'],
'b' : ['a'],
'c' : ['a','b','c']
}) == False # d11
assert is_symmetric_adj({ 'a' : ['b', 'c'],
'b' : ['a','c'],
'c' : ['a','b','c']
}) == True # d12
Surjective relations
If we consider a graph as a nxn binary relation where the domain is the same as the codomain, such relation is called surjective if every node is reached by at least one edge.
For example, G1 here is surjective, because there is at least one edge reaching into each node (self-loops as in 0 node also count as incoming edges)
[11]:
G1 = [
[True, True, False, False],
[False, False, False, True],
[False, True, True, False],
[False, True, True, True],
]
[12]:
draw_mat(G1)

G2 down here instead does not represent a surjective relation, as there is at least one node ( 2 in our case) which does not have any incoming edge:
[13]:
G2 = [
[True, True, False, False],
[False, False, False, True],
[False, True, False, False],
[False, True, False, False],
]
[14]:
draw_mat(G2)

Exercise - surjective
✪✪ RETURN True if provided graph mat as list of boolean lists is an nxn surjective binary relation, otherwise return False
[15]:
def surjective(mat):
raise Exception('TODO IMPLEMENT ME !')
m1 = [ [False] ]
assert surjective(m1) == False
m2 = [ [True] ]
assert surjective(m2) == True
m3 = [ [True, False],
[False, False] ]
assert surjective(m3) == False
m4 = [ [False, True],
[False, False] ]
assert surjective(m4) == False
m5 = [ [False, False],
[True, False] ]
assert surjective(m5) == False
m6 = [ [False, False],
[False, True] ]
assert surjective(m6) == False
m7 = [ [True, False],
[True, False] ]
assert surjective(m7) == False
m8 = [ [True, False],
[False, True] ]
assert surjective(m8) == True
m9 = [ [True, True],
[False, True] ]
assert surjective(m9) == True
m10 = [ [True, True, False, False],
[False, False, False, True],
[False, True, False, False],
[False, True, False, False] ]
assert surjective(m10) == False
m11 = [ [True, True, False, False],
[False, False, False, True],
[False, True, True, False],
[False, True, True, True] ]
assert surjective(m11) == True
Further resources
Rule based design by Lex Wedemeijer, Stef Joosten, Jaap van der woude: a very readable text on how to represent information using only binary relations with boolean matrices. This a theorical book with no python exercise so it is not a mandatory read, it only gives context and practical applications for some of the material on graphs presented during the course
Continue
Go on with simple statistics