Relational data 3 - simple statistics
Download exercises zip
We will now compute and visualize simple statistics about graphs (they don’t require node discovery algorithms).
What to do
unzip exercises in a folder, you should get something like this:
relational
relational1-intro.ipynb
relational1-intro-sol.ipynb
relational2-binrel.ipynb
relational2-binrel-sol.ipynb
relational3-simple-stats.ipynb
relational3-simple-stats-sol.ipynb
relational4-chal.ipynb
jupman.py
soft.py
WARNING: to correctly visualize the notebook, it MUST be in an unzipped folder !
open Jupyter Notebook from that folder. Two things should open, first a console and then browser. The browser should show a file list: navigate the list and open the notebook
relational/relational3-simple-stats.ipynb
WARNING 2: DO NOT use the Upload button in Jupyter, instead navigate in Jupyter browser to the unzipped folder !
Go on reading that notebook, and follow instuctions inside.
Shortcut keys:
to execute Python code inside a Jupyter cell, press
Control + Enterto execute Python code inside a Jupyter cell AND select next cell, press
Shift + Enterto execute Python code inside a Jupyter cell AND a create a new cell aftwerwards, press
Alt + EnterIf the notebooks look stuck, try to select
Kernel -> Restart
Outdegrees and indegrees
The out-degree \(\deg^+(v)\) of a node \(v\) is the number of edges going out from it, while the in-degree \(\deg^-(v)\) is the number of edges going into it.
NOTE: the out-degree and in-degree are not the sum of weights ! They just count presence or absence of edges.
For example, consider this graph:
[2]:
from soft import draw_adj
d = {
'a' : ['b','c'],
'b' : ['b','d'],
'c' : ['a','b','c','d'],
'd' : ['b','d']
}
draw_adj(d)
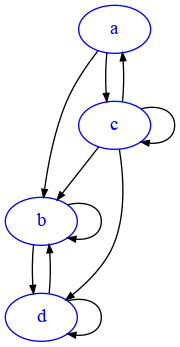
The out-degree of d is 2, because it has one outgoing edge to b but also an outgoing edge to itself. The indegree of d is 3, because it has an edge coming from b, one from c and one self-loop from d itself.
Exercise - outdegree_adj
✪ RETURN the outdegree of a node from graph d represented as a dictionary of adjacency lists
If
vis not a vertex ofd, raiseValueError
[3]:
def outdegree_adj(d, v):
raise Exception('TODO IMPLEMENT ME !')
try:
outdegree_adj({'a':[]},'b')
raise Exception("SHOULD HAVE FAILED !")
except ValueError:
"passed test"
d1 = { 'a':[] }
assert outdegree_adj(d1,'a') == 0
d2 = { 'a':['a'] }
assert outdegree_adj(d2,'a') == 1
d3 = { 'a':['a','b'],
'b':[] }
assert outdegree_adj(d3,'a') == 2
d4 = { 'a':['a','b'],
'b':['a','b','c'],
'c':[] }
assert outdegree_adj(d4,'b') == 3
Exercise - outdegree_mat
✪✪ RETURN the outdegree of a node i from a graph boolean matrix \(n\) x \(n\) represented as a list of lists
If
iis not a node of the graph, raiseValueError
[4]:
def outdegree_mat(mat, i):
raise Exception('TODO IMPLEMENT ME !')
try:
outdegree_mat([[False]],7)
raise Exception("SHOULD HAVE FAILED !")
except ValueError:
"passed test"
try:
outdegree_mat([[False]],-1)
raise Exception("SHOULD HAVE FAILED !")
except ValueError:
"passed test"
m1 = [ [False] ]
assert outdegree_mat( m1, 0) == 0
m2 = [ [True] ]
assert outdegree_mat( m2, 0) == 1
m3 = [ [True, True],
[False, False] ]
assert outdegree_mat( m3, 0) == 2
m4 = [ [True, True, False],
[True, True, True],
[False, False, False] ]
assert outdegree_mat(m4,1) == 3
Exercise - outdegree_avg
✪✪ RETURN the average outdegree of nodes in graph d, represented as dictionary of adjacency lists.
Assume all nodes are in the keys.
[5]:
def outdegree_avg(d):
raise Exception('TODO IMPLEMENT ME !')
d1 = { 'a':[] }
assert outdegree_avg(d1) == 0
d2 = { 'a':['a'] }
assert round( outdegree_avg(d2), 2) == 1.00 / 1.00
d3 = { 'a':['a','b'],
'b':[] }
assert round( outdegree_avg(d3), 2) == (2 + 0) / 2
d4 = { 'a':['a','b'],
'b':['a','b','c'],
'c':[] }
assert round( outdegree_avg(d4), 2) == round( (2 + 3) / 3 , 2)
Exercise - indegree_adj
The indegree of a node v is the number of edges going into it.
✪✪ RETURN the indegree of node v in graph d, represented as a dictionary of adjacency lists
If
vis not a node of the graph, raiseValueError
[6]:
def indegree_adj(d, v):
raise Exception('TODO IMPLEMENT ME !')
try:
indegree_adj({'a':[]},'b')
raise Exception("SHOULD HAVE FAILED !")
except ValueError:
"passed test"
d1 = { 'a':[] }
assert indegree_adj(d1,'a') == 0
d2 = {'a':['a']}
assert indegree_adj(d2,'a') == 1
d3 = { 'a':['a','b'],
'b':[]}
assert indegree_adj(d3, 'a') == 1
d4 = { 'a':['a','b'],
'b':['a','b','c'],
'c':[]}
assert indegree_adj(d4, 'b') == 2
Exercise - indegree_mat
✪✪ RETURN the indegree of a node i from a graph boolean matrix nxn represented as a list of lists
If
iis not a node of the graph, raiseValueError
[7]:
def indegree_mat(mat, i):
raise Exception('TODO IMPLEMENT ME !')
try:
indegree_mat([[False]],7)
raise Exception("SHOULD HAVE FAILED !")
except ValueError:
"passed test"
assert indegree_mat(
[
[False]
]
,0) == 0
m1 = [ [True] ]
assert indegree_mat(m1, 0) == 1
m2 = [ [True, True],
[False, False] ]
assert indegree_mat(m2, 0) == 1
m3 = [ [True, True, False],
[True, True, True],
[False, False, False] ]
assert indegree_mat( m3, 1) == 2
Exercise - indegree_avg
✪✪ RETURN the average indegree of nodes in graph d, represented as dictionary of adjacency lists.
Assume all nodes are in the keys
[8]:
def indegree_avg(d):
raise Exception('TODO IMPLEMENT ME !')
d1 = { 'a':[] }
assert indegree_avg(d1) == 0
d2 = { 'a':['a'] }
assert round( indegree_avg(d2), 2) == 1.00 / 1.00
d3 = { 'a':['a','b'],
'b':[]}
assert round( indegree_avg(d3), 2) == (1 + 1) / 2
d4 = { 'a':['a','b'],
'b':['a','b','c'],
'c':[]}
assert round( indegree_avg(d4), 2) == round( (2 + 2 + 1) / 3 , 2)
Was it worth it?
QUESTION: Is there any difference between the results of indegree_avg and outdegree_avg ?
networkx Indegrees and outdegrees
With Networkx we can easily calculate indegrees and outdegrees of a node:
[9]:
import networkx as nx
# notice with networkx if nodes are already referenced to in an adjacency list
# you do not need to put them as keys:
G=nx.DiGraph({
'a':['b','c'], # node a links to b and c
'b':['b','c', 'd'] # node b links to b itself, c and d
})
draw_nx(G)

[10]:
G.out_degree('a')
[10]:
2
QUESTION: What is the outdegree of 'b' ? Try to think about it and then confirm your thoughts with networkx:
[11]:
# write here
QUESTION: We defined indegree and outdegree. Can you guess what the degree might be ? In particular, for a self pointing node like 'b', what could it be? Try to use G.degree('b') methods to validate your thoughts.
[12]:
# write here
[13]:
# write here
Visualizing distributions
We will try to study the distributions visually. Let’s take an example networkx DiGraph:
[14]:
import networkx as nx
G1=nx.DiGraph({
'a':['b','c'],
'b':['b','c', 'd'],
'c':['a','b','d'],
'd':['b', 'd']
})
draw_nx(G1)

indegree per node
✪✪ Display a plot for graph G where the xtick labels are the nodes, and the y is the indegree of those nodes.
Note: instead of xticks you might directly use categorical variables IF you have matplotlib >= 2.1.0
Here we use xticks as sometimes you might need to fiddle with them anyway
Expected result:
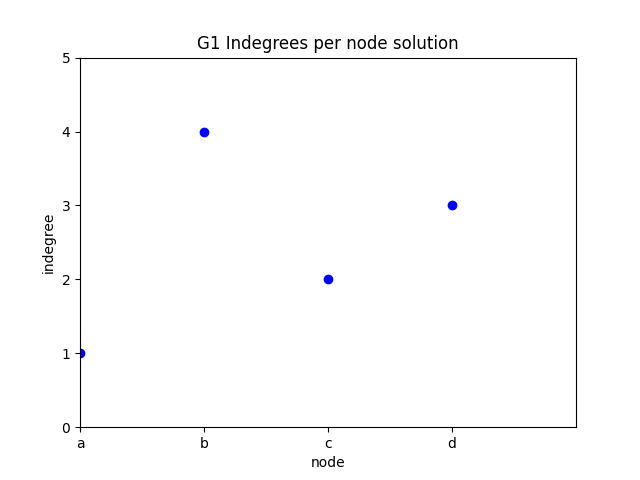
To get the nodes, you can use the G1.nodes() function:
[15]:
G1.nodes()
[15]:
NodeView(('a', 'b', 'c', 'd'))
It gives back a NodeView which is not a list, but still you can iterate through it with a for in cycle:
[16]:
for n in G1.nodes():
print(n)
a
b
c
d
Also, you can get the indegree of a node with
[17]:
G1.in_degree('b')
[17]:
4
[18]:
# write here
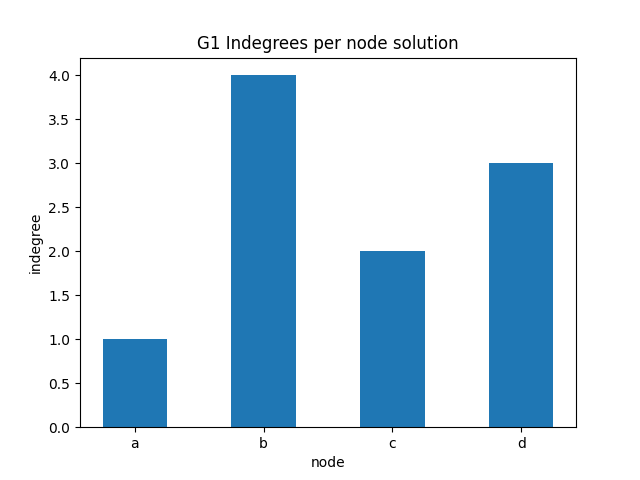
indegree per node bar plot
The previous plot with dots doesn’t look so good - we might try to use instead a bar plot. First look at this example, then proceed with the exercise
✪✪ Display a bar plot for graph G1 where the xtick labels are the nodes, and the y is the indegree of those nodes.
Expected result:
[19]:
# write here
indegree per node sorted alphabetically
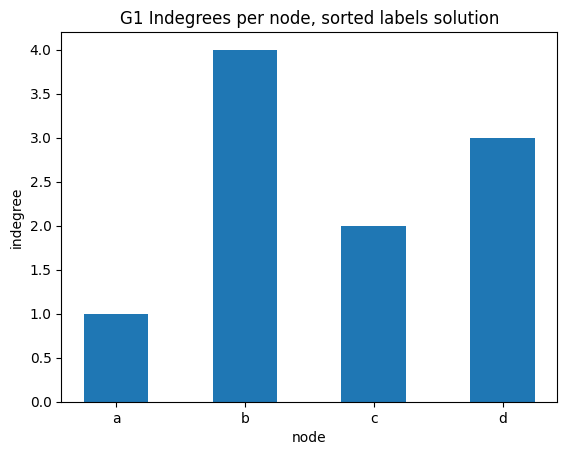
✪✪ Display the same bar plot as before, but now sort nodes alphabetically.
NOTE: you cannot run .sort() method on the result given by G1.nodes(), because nodes in network by default have no inherent order. To use .sort() you need first to convert the result to a list object.
You should get something like this:

[20]:
# write here
[21]:
# write here
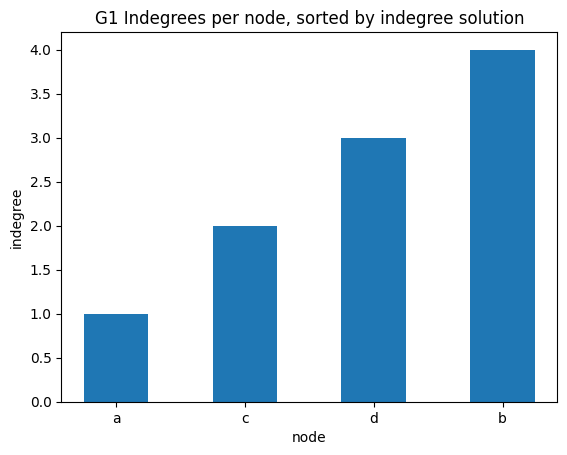
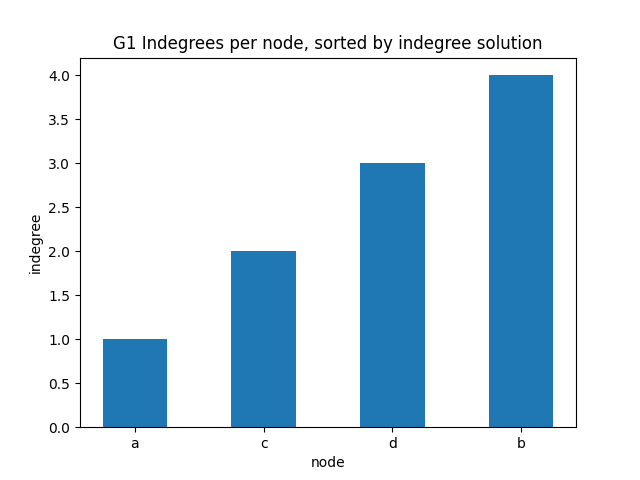
indegree per node sorted
✪✪✪ Display the same bar plot as before, but now sort nodes according to their indegree. This is more challenging, to do it you need to use some sort trick.
HINT: first read the Python documentation
Expected result:
[22]:
# write here
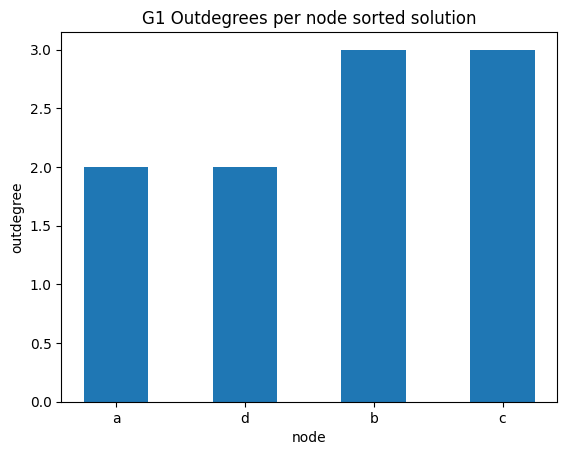
out degrees per node sorted
✪✪✪ Do the same graph as before for the outdegrees.
Expected result:
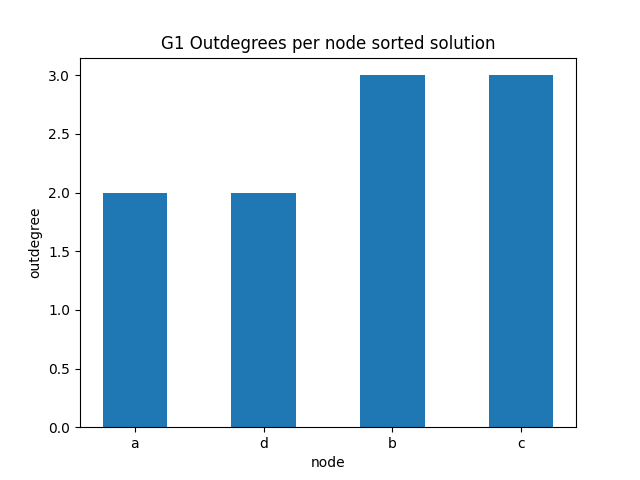
You can get the outdegree of a node with:
[23]:
G1.out_degree('b')
[23]:
3
[24]:
# write here
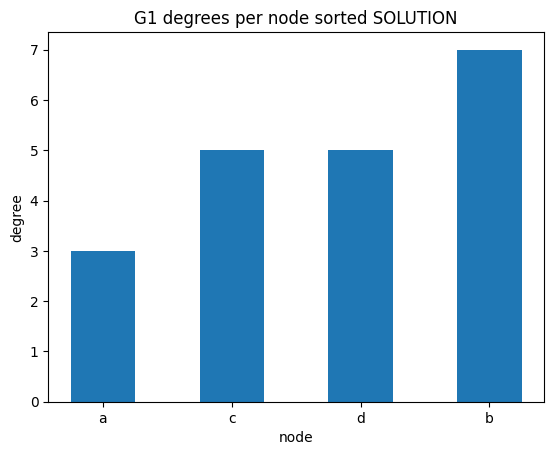
degrees per node
✪✪✪ We might check as well the sorted degrees per node, intended as the sum of in_degree and out_degree. To get the sum, use G1.degree(node) function.
Expected result:
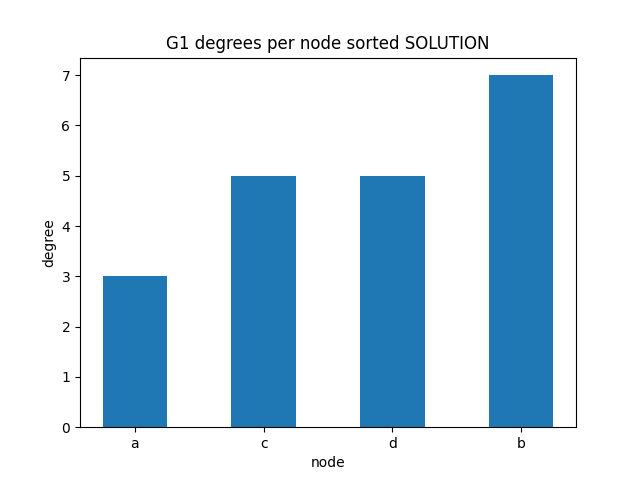
[25]:
# write here
In out degrees per node
✪✪✪✪ Look at this example, and make a double bar chart sorting nodes by their total degree. To do so, in the tuples you will need vertex, in_degree, out_degree and also degree.
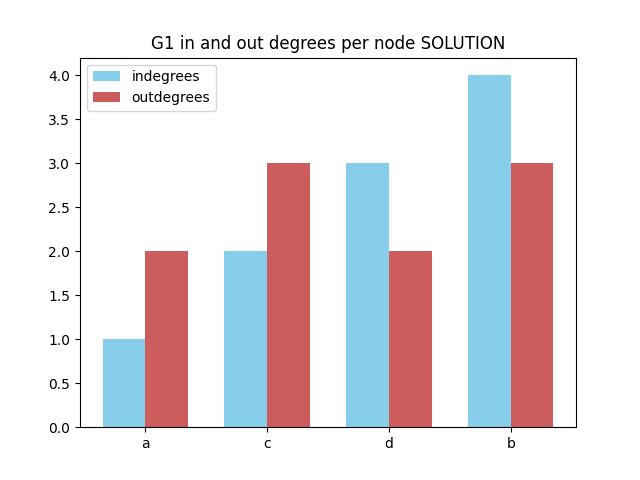
[26]:
# write here
Frequency histogram
Now let’s try drawing degree frequencies: for each degree present in the graph we want to display a bar as high as the number of times that particular degree appears.
For doing so, we will need a matplot histogram, see documentation
We will need to tell matplotlib how many columns we want, which in histogram terms are called bins. We also need to give the histogram a series of numbers so it can count how many times each number occurs. Let’s consider this graph G2:
[27]:
import networkx as nx
G2=nx.DiGraph({
'a':['b','c'],
'b':['b','c', 'd'],
'c':['a','b','d'],
'd':['b', 'd','e'],
'e':[],
'f':['c','d','e'],
'g':['e','g']
})
draw_nx(G2)
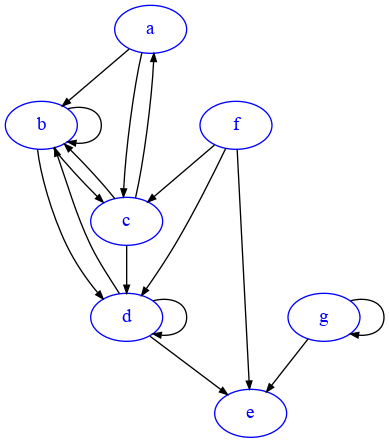
If we take the degree sequence of G2 we get this:
[28]:
degrees_G2 = [G2.degree(n) for n in G2.nodes()]
degrees_G2
[28]:
[3, 7, 6, 7, 3, 3, 3]
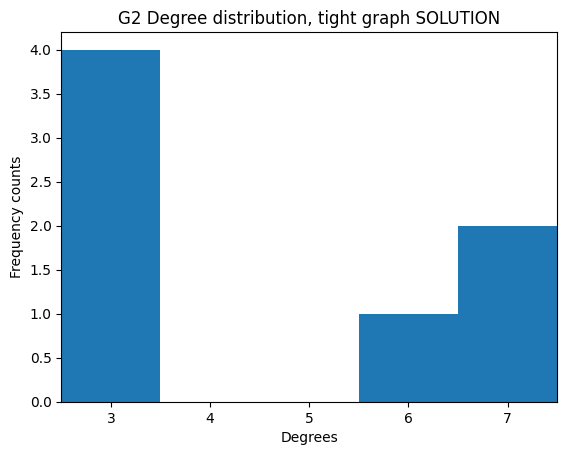
We see 3 appears four times, 6 once, and 7 twice.
Let’s find a good number for the bins. First we can check the boundaries our x axis should have:
[29]:
min(degrees_G2)
[29]:
3
[30]:
max(degrees_G2)
[30]:
7
So on the x axis our histogram must go at least from 3 and at least to 7. If we want integer columns (bins), we will need at least ticks for going from 3 included to 7 included, that is at least ticks for 3,4,5,6,7. For precise display, when we have integer x it’s best to also manually provide the sequence of bin edges, remembering it should start at least from the minimum included (in our case, 3) and arrive to the maximum + 1 included (in our case,
7 + 1 = 8)
NOTE: precise histogram drawing can be quite tricky, please do read this StackOverflow post for more details about it.
[31]:
import matplotlib.pyplot as plt
import numpy as np
degrees = [G2.degree(n) for n in G2.nodes()]
# add histogram
# in this case hist returns a tuple of three values
# we put in three variables
n, bins, columns = plt.hist(degrees_G2,
bins=range(3,9), # 3 *included*, 4,5,6,7,8 *included*
width=1.0) # graphical bars width
plt.xlabel('Degrees')
plt.ylabel('Frequency counts')
plt.title('G2 Degree distribution')
plt.xlim(0, max(degrees) + 2)
plt.show()
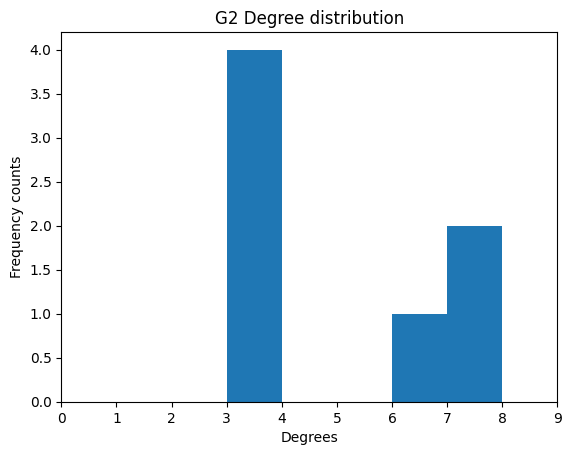
As expected, we see 3 is counted four times, 6 once, and 7 twice.
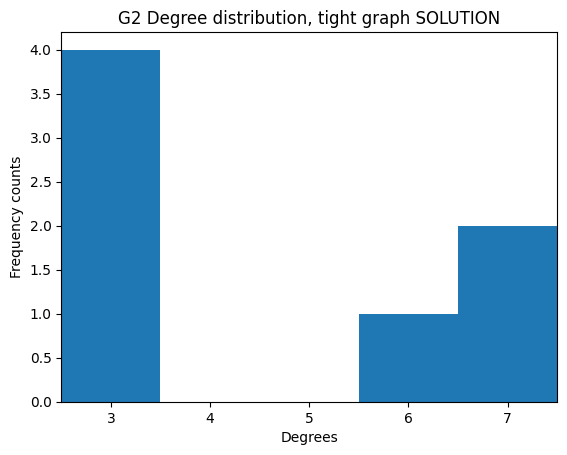
Exercise - better histogram display
✪✪✪ Still, it would be visually better to align the x ticks to the middle of the bars with xticks, and also to make the graph tighter by setting the xlim appropriately. This is not always easy to do.
Read carefully this StackOverflow post and try doing it by yourself.
NOTE: set one thing at a time and try if it works(i.e. first xticks and then xlim), doing everything at once might get quite confusing.
Expected result:

[32]:
# write here
Graph models
Let’s study frequencies of some known network types.
Exercise - Erdős–Rényi model
✪✪ A simple graph model we can think of is the so-called Erdős–Rényi model: it’s an undirected graph where have n nodes, and each node is connected to each other with probability p. In networkx, we can generate a random one by issuing this command:
[33]:
G = nx.erdos_renyi_graph(10, 0.5)
In the drawing, the absence of arrows confirms it’s undirected:
[34]:
draw_nx(G)
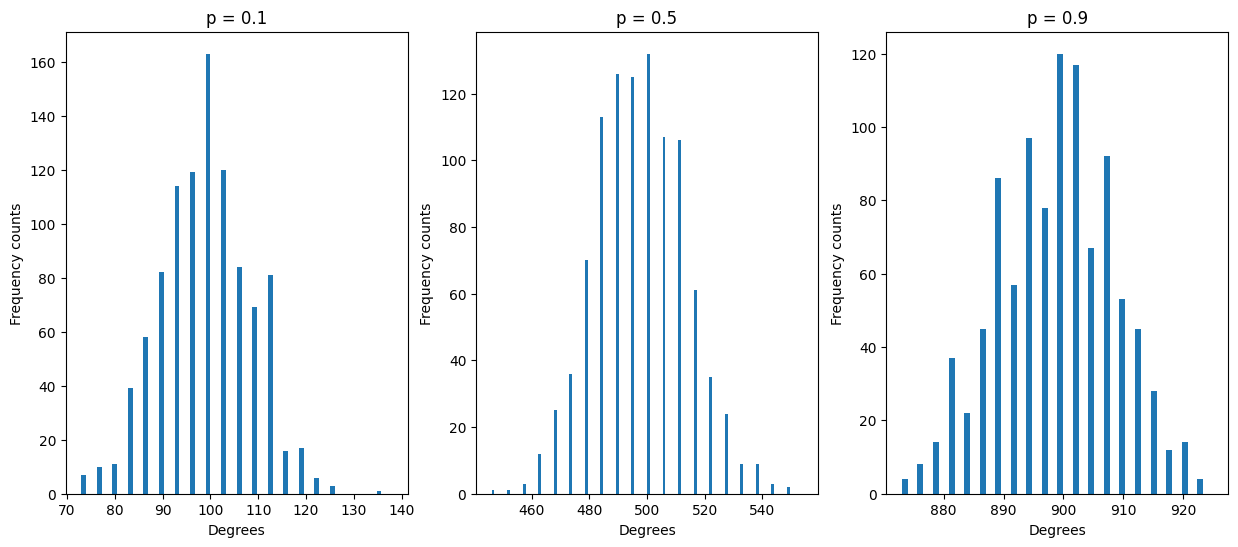
Try plotting degree distribution for different values of p (0.1, 0.5, 0.9) with a fixed n=1000, putting them side by side on the same row. What does their distribution look like ? Where are they centered ?
to put them side by side, look at this example
to avoid rewriting the same code again and again, define a
plot_erdos(n,p,j)function to be called three times.
Expected result:

[35]:
# write here
Continue
Go on with the challenges