Matrices 2: list of lists - other exercises
Download exercises zip
As always the only true way to understand a topic is by doing more exercises, so here they are!
What to do
unzip exercises in a folder, you should get something like this:
matrices-lists
matrices-lists1.ipynb
matrices-lists1-sol.ipynb
matrices-lists2.ipynb
matrices-lists2-sol.ipynb
matrices-lists3-chal.ipynb
jupman.py
WARNING: to correctly visualize the notebook, it MUST be in an unzipped folder !
open Jupyter Notebook from that folder. Two things should open, first a console and then browser. The browser should show a file list: navigate the list and open the notebook
matrices-lists/matrices-lists2.ipynbGo on reading that notebook, and follow instuctions inside.
Shortcut keys:
to execute Python code inside a Jupyter cell, press
Control + Enterto execute Python code inside a Jupyter cell AND select next cell, press
Shift + Enterto execute Python code inside a Jupyter cell AND a create a new cell aftwerwards, press
Alt + EnterIf the notebooks look stuck, try to select
Kernel -> Restart
Exercise - diag
diag extracts the diagonal of a matrix. To do so, diag requires an nxn matrix as input. To make sure we actually get an nxn matrix, this time you will have to validate the input, that is check if the number of rows is equal to the number of columns (as always we assume the matrix has at least one row and at least one column). If the matrix is not nxn, the function should stop raising an exception. In particular, it shoud raise a
ValueError, which is the standard Python exception to raise when the expected input is not correct and you can’t find any other more specific error.
Just for illustrative puroposes, we show here the index numbers i and j and avoid putting apices around strings:
\ j 0,1,2,3
i
[
0 [a,b,c,d],
1 [e,f,g,h],
2 [p,q,r,s],
3 [t,u,v,z]
]
Let’s see a step by step execution:
\ j 0,1,2,3
i
[
extract from row at i=0 --> 0 [a,b,c,d], 'a' is extracted from mat[0][0]
1 [e,f,g,h],
2 [p,q,r,s],
3 [t,u,v,z]
]
\ j 0,1,2,3
i
[
0 [a,b,c,d],
extract from row at i=1 --> 1 [e,f,g,h], 'f' is extracted from mat[1][1]
2 [p,q,r,s],
3 [t,u,v,z]
]
\ j 0,1,2,3
i
[
0 [a,b,c,d],
1 [e,f,g,h],
extract from row at i=2 --> 2 [p,q,r,s], 'r' is extracted from mat[2][2]
3 [t,u,v,z]
]
\ j 0,1,2,3
i
[
0 [a,b,c,d],
1 [e,f,g,h],
2 [p,q,r,s],
extract from row at i=3 --> 3 [t,u,v,z] 'z' is extracted from mat[3][3]
]
From the above, we notice we need elements from these indeces:
i, j
1, 1
2, 2
3, 3
There are two ways to solve this exercise, one is to use a double for (a nested for to be precise) while the other method uses only one for. Try to solve it in both ways. How many steps do you need with double for? and with only one?
✪✪ EXERCISE: Implement the diag function, which given an nxn matrix mat as a list of lists, RETURN a list which contains the elemets in the diagonal (top left to bottom right corner).
if
matis notnxnraiseValueError
[2]:
def diag(mat):
raise Exception('TODO IMPLEMENT ME !')
# TEST START - DO NOT TOUCH!
# if you wrote the whole code correct, and execute the cell, Python shouldn't raise `AssertionError`
m = [ ['a','b','c'],
['d','e','f'],
['g','h','i'] ]
assert diag(m) == ['a','e','i']
try:
diag([ ['a','b'] ]) # 1x2 dimension, not square
raise Exception("SHOULD HAVE FAILED !") # if diag raises an exception which is ValueError as we
# expect it to do, the code should never arrive here
except ValueError: # this only catches ValueError. Other types of errors are not catched
pass # In an except clause you always need to put some code.
# Here we put a placeholder just to fill in
# TEST END
Exercise - anti_diag
✪✪ Given an nxn matrix mat as a list of lists, RETURN a list which contains the elemets in the antidiagonal (top right to bottom left corner).
If mat is not
nxnraiseValueError
Before implementing it, be sure to write down understand the required indeces as we did in the example for the diag function.
Show solution[3]:
def anti_diag(mat):
raise Exception('TODO IMPLEMENT ME !')
m = [ ['a','b','c'],
['d','e','f'],
['g','h','i'] ]
assert anti_diag(m) == ['c','e','g']
# If you have doubts about the indexes remember to try it in python tutor !
# jupman.pytut()
Exercise - is_utriang
✪✪✪ You will now try to iterate only the lower triangular half of a matrix. Let’s look at an example:
[4]:
m = [
[3,2,5,8],
[0,6,2,3],
[0,0,4,9],
[0,0,0,5]
]
Just for illustrative puroposes, we show here the index numbers i and j:
\ j 0,1,2,3
i
[
0 [3,2,5,8],
1 [0,6,2,3],
2 [0,0,4,9],
3 [0,7,0,5]
]
Let’s see a step by step execution an a non-upper triangular matrix:
\ j 0,1,2,3
i
[
0 [3,2,5,8],
start from row at index i=1 -> 1 [0,6,2,3], Check until column limit j=0 included
2 [0,0,4,9],
3 [0,7,0,5]
]
One zero is found, time to check next row.
\ j 0,1,2,3
i
[
0 [3,2,5,8],
1 [0,6,2,3],
check row at index i=2 ---> 2 [0,0,4,9], Check until column limit j=1 included
3 [0,7,0,5]
]
Two zeros are found. Time to check next row.
\ j 0,1,2,3
i
[
0 [3,2,5,8],
1 [0,6,2,3],
2 [0,0,4,9],
check row at index i=3 ---> 3 [0,7,0,5] Check until column limit j=2 included
] BUT can stop sooner at j=1 because
number at j=1 is different from zero.
As soon as 7 is found, can return False
In this case the matrix is not upper
triangular
VII COMMANDMENT You shall also write on paper!
When you develop these algorithms, it is fundamental to write down a step by step example like the above to get a clear picture of what is happening. Also, if you write down the indeces correctly, you will easily be able to derive a generalization. To find it, try to further write the found indeces in a table.
For example, from above for each row index i we can easily find out which limit index j we need to reach for our hunt for zeros:
i |
limit j (included) |
Notes |
|---|---|---|
1 |
0 |
we start from row at index i=1 |
2 |
1 |
|
3 |
2 |
From the table, we can see the limit for j can be calculated in terms of the current row index i with the simple formula i - 1
The fact you need to span through rows and columns suggest you need two fors, one for rows and one for columns - that is, a nested for.
please use ranges of indexes to carry out the task (no
for row in mat..)please use letter
ias index for rows,jas index of columns and in case you need itnletter as matrix dimension
HINT 1: remember you can set range to start from a specific index, like range(3,7) will start from 3 and end to 6 included (last 7 is excluded!)
HINT 2: To implement this, it’s best looking for numbers different from zero. As soon as you find one, you can stop the function and return False. Only after all the number checking is done you can return True.
Finally, be reminded of the following:
II COMMANDMENT Whenever you introduce a variable with a for cycle, such variable must be new
If you defined a variable before, you shall not reintroduce it in a for, since it’s confusing and error prone.
So avoid these sins:
[5]:
i = 7
for i in range(3): # sin, you lose i variable
print(i)
0
1
2
[6]:
def f(i):
for i in range(3): # sin again, you lose i parameter
print(i)
[7]:
for i in range(2):
for i in range(3): # debugging hell, you lose i from outer for
print(i)
0
1
2
0
1
2
✪✪✪ EXERCISE: If you read all the above, start implementing the function is_utriang, which RETURN True if the provided nxn matrix is upper triangular, that is, has all the entries below the diagonal set to zero. Return False otherwise.
[8]:
def is_utriang(mat):
raise Exception('TODO IMPLEMENT ME !')
assert is_utriang([ [1] ]) == True
assert is_utriang([ [3,2,5],
[0,6,2],
[0,0,4] ]) == True
assert is_utriang([ [3,2,5],
[0,6,2],
[1,0,4] ]) == False
assert is_utriang([ [3,2,5],
[0,6,2],
[1,1,4] ]) == False
assert is_utriang([ [3,2,5],
[0,6,2],
[0,1,4] ]) == False
assert is_utriang([ [3,2,5],
[1,6,2],
[1,0,4] ]) == False
Exercise - stitch_left_mod
This time let’s try to modify mat1 in place, by stitching mat2 to the left of mat1.
So this time don’t put a return instruction.
You will need to perform list insertion, which can be tricky. There are many ways to do it in Python, one could be using the weird splice assignment insertion:
mylist[0:0] = list_to_insert
see here for more info: https://stackoverflow.com/a/10623383
✪✪✪ EXERCISE: Implement stitch_left_mod, which given the matrices mat1 and mat2 as list of lists, with mat1 of size n x l and mat2 of size n x r, MODIFIES mat1 so that it becomes of size n x (l + r), by stitching second mat2 to the left of mat1
[9]:
def stitch_left_mod(mat1,mat2):
raise Exception('TODO IMPLEMENT ME !')
m1 = [ ['a','b','c'],
['d','b','a'] ]
m2 = [ ['f','b'],
['g','h'] ]
res = [ ['f','b','a','b','c'],
['g','h','d','b','a'] ]
stitch_left_mod(m1, m2)
assert m1 == res
Exercise - transpose_1
Let’s see how to transpose a matrix in-place. The transpose \(M^T\) of a matrix \(M\) is defined as
\(M^T[i][j] = M[j][i]\)
The definition is simple yet implementation might be tricky. If you’re not careful, you could easily end up swapping the values twice and get the same original matrix. To prevent this, iterate only the upper triangular part of the matrix and remember range funciton can also have a start index:
[10]:
list(range(3,7))
[10]:
[3, 4, 5, 6]
Also, make sure you know how to swap just two values by solving first this very simple exercise - also check the result in Python Tutor
Show solution[11]:
x = 3
y = 7
# write here code for swapping x and y (don't directly use the constants 3 and 7!)
Going back to the transpose, for now we will consider only an nxn matrix. To make sure we actually get an nxn matrix, we will validate the input as before.
IV COMMANDMENT (adapted for matrices): You shall never ever reassign function parameters
def myfun(M):
# M is a parameter, so you shall *not* do any of such evil:
M = [
[6661,6662],
[6663,6664 ]
]
# For the sole case of composite parameters like lists (or lists of lists ..)
# you can write stuff like this IF AND ONLY IF the function specification
# requires you to modify the parameter internal elements (i.e. transposing _in-place_):
M[0][1] = 6663
✪✪✪ EXERCISE If you read all the above, you can now proceed implementing the transpose_1 function, which MODIFIES the given nxn matrix mat by transposing it in-place.
If the matrix is not
nxn, raises aValueError
[12]:
def transpose_1(mat):
raise Exception('TODO IMPLEMENT ME !')
# let's try wrong matrix dimensions:
try:
transpose_1([ [3,5] ])
raise Exception("SHOULD HAVE FAILED !")
except ValueError:
pass
m1 = [ ['a'] ]
transpose_1(m1)
assert m1 == [ ['a'] ]
m2 = [ ['a','b'],
['c','d'] ]
transpose_1(m2)
assert m2 == [ ['a','c'],
['b','d'] ]
Exercise - transpose_2
✪✪ Now let’s try to transpose a generic nxm matrix. This time for simplicity we will return a whole new matrix.
RETURN a NEW mxn matrix which is the transpose of the given nxm matrix mat as list of lists.
[13]:
def transpose_2(mat):
raise Exception('TODO IMPLEMENT ME !')
m1 = [ ['a'] ]
r1 = transpose_2(m1)
assert r1 == [ ['a'] ]
r1[0][0] = 'z'
assert m1[0][0] == 'a'
m2 = [ ['a','b','c'],
['d','e','f'] ]
assert transpose_2(m2) == [ ['a','d'],
['b','e'],
['c','f'] ]
Exercise - cirpillino
Given a string and an integer n, RETURN a NEW matrix as list of lists containing all the characters in string subdivided in rows of n elements each.
if the string length is not exactly divisible by
n, raisesValueError
Example:
>>> cirpillino('cirpillinozimpirelloulalimpo', 4)
[['c', 'i', 'r', 'p'],
['i', 'l', 'l', 'i'],
['n', 'o', 'z', 'i'],
['m', 'p', 'i', 'r'],
['e', 'l', 'l', 'o'],
['u', 'l', 'a', 'l'],
['i', 'm', 'p', 'o']]
[14]:
def cirpillino(string, n):
raise Exception('TODO IMPLEMENT ME !')
# TEST
assert cirpillino('z', 1) == [['z']]
assert cirpillino('abc', 1) == [['a'],
['b'],
['c']]
assert cirpillino('abcdef', 2) == [['a','b'],
['c','d'],
['e','f']]
assert cirpillino('abcdef', 3) == [['a','b','c'],
['d','e','f']]
assert cirpillino('cirpillinozimpirelloulalimpo', 4) == [['c', 'i', 'r', 'p'],
['i', 'l', 'l', 'i'],
['n', 'o', 'z', 'i'],
['m', 'p', 'i', 'r'],
['e', 'l', 'l', 'o'],
['u', 'l', 'a', 'l'],
['i', 'm', 'p', 'o']]
try:
cirpillino('abc', 5)
raise Exception("I should have failed!")
except ValueError:
pass
Exercise - flag
Given two integer numbers n and m, with m a multiple of 3, RETURN a matrix n x m as a list of lists having cells filled with numbers from 0 to 2 divided in three vertical stripes.
if
mis not a multiple of3, raisesValueError
Example:
>>> flag(5,12)
[[0, 0, 0, 0, 1, 1, 1, 1, 2, 2, 2, 2],
[0, 0, 0, 0, 1, 1, 1, 1, 2, 2, 2, 2],
[0, 0, 0, 0, 1, 1, 1, 1, 2, 2, 2, 2],
[0, 0, 0, 0, 1, 1, 1, 1, 2, 2, 2, 2],
[0, 0, 0, 0, 1, 1, 1, 1, 2, 2, 2, 2]]
[15]:
def flag(n,m):
raise Exception('TODO IMPLEMENT ME !')
# TEST
assert flag(1,3) == [[0, 1, 2]]
assert flag(1,6) == [[0,0,1,1, 2,2]]
assert flag(4,6) == [[0, 0, 1, 1, 2, 2],
[0, 0, 1, 1, 2, 2],
[0, 0, 1, 1, 2, 2],
[0, 0, 1, 1, 2, 2]]
assert flag(2,9) == [[0, 0, 0, 1, 1, 1, 2, 2, 2],
[0, 0, 0, 1, 1, 1, 2, 2, 2]]
assert flag(5,12) == [[0, 0, 0, 0, 1, 1, 1, 1, 2, 2, 2, 2],
[0, 0, 0, 0, 1, 1, 1, 1, 2, 2, 2, 2],
[0, 0, 0, 0, 1, 1, 1, 1, 2, 2, 2, 2],
[0, 0, 0, 0, 1, 1, 1, 1, 2, 2, 2, 2],
[0, 0, 0, 0, 1, 1, 1, 1, 2, 2, 2, 2]]
try:
flag(3,7)
raise Exception("I should have failed!")
except ValueError:
pass
Exercise - avoid_diag
✪✪ Given a sqaure matrix \(n\) x \(n\) as a list of lists, RETURN a NEW list with the sum of all numbers of every row EXCEPT the diagonal
if the matrix is not square, raise
ValueError
Example:
>>> avoid_diag([ [5,6,2],
[4,7,9],
[1,9,8]])
[8, 13, 10]
because
8 = 6 + 2
13 = 4 + 7
10 = 1 + 9
[16]:
def avoid_diag(mat):
raise Exception('TODO IMPLEMENT ME !')
assert avoid_diag([[5]]) == [0]
m2 = [[5,7],
[9,1]]
assert avoid_diag(m2) == [7,9]
assert m2 == [[5,7],
[9,1]]
assert avoid_diag([ [5,6,2],
[4,7,9],
[1,9,8]]) == [8, 13, 10]
try:
avoid_diag([[2,3,5],
[1,5,2]])
raise Exception("I should have failed!")
except ValueError:
pass
Exercise - no_diag
✪✪ Given a matrix \(n\) x \(n\) as a list of lists, RETURN a NEW matrix \(n\) x \(n\)-1 having the same cells as the original one EXCEPT the cells in the diagonal.
if the matrix is not squared, raises
ValueError
Example:
>>> m = [[8,5,3,4],
[7,2,4,1],
[9,8,3,5],
[6,0,4,7]]
>>> no_diag(m)
[[5,3,4],
[7,4,1],
[9,8,5],
[6,0,4]]
[17]:
def no_diag(mat):
raise Exception('TODO IMPLEMENT ME !')
# TEST
m1 = [[3,4],
[8,7]]
assert no_diag(m1) == [[4],
[8]]
assert m1 == [[3,4], # verify the original was not changed
[8,7]]
m2 = [[9,4,3],
[8,5,6],
[0,2,7]]
assert no_diag(m2) == [[4,3],
[8,6],
[0,2]]
m3 = [[8,5,3,4],
[7,2,4,1],
[9,8,3,5],
[6,0,4,7]]
assert no_diag(m3) == [[5,3,4],
[7,4,1],
[9,8,5],
[6,0,4]]
try:
no_diag([[2,3,5],
[1,5,2]])
raise Exception("I should have failed!")
except ValueError:
pass
Exercise - no_anti_diag
✪✪✪ Given a ✪✪ Given a matrix \(n\) x \(n\) as a list of lists, RETURN a NEW matrix n x n-1 having the same cells as the original one EXCEPT the cells in the ANTI-diagonal. For examples, see asserts.
if the matrix is not squared, raises
ValueError
[18]:
def no_anti_diag(mat):
raise Exception('TODO IMPLEMENT ME !')
m1 = [[3,4],
[8,7]]
assert no_anti_diag(m1) == [[3],
[7]]
assert m1 == [[3,4], # verify the original was not changed
[8,7]]
m2 = [[9,4,3],
[8,5,6],
[0,2,7]]
assert no_anti_diag(m2) == [[9,4],
[8,6],
[2,7]]
m3 = [[8,5,3,4],
[7,2,4,1],
[9,8,3,5],
[6,0,4,7]]
assert no_anti_diag(m3) == [[8,5,3],
[7,2,1],
[9,3,5],
[0,4,7]]
try:
no_anti_diag([[2,3,5],
[1,5,2]])
raise Exception("I should have failed!")
except ValueError:
pass
Exercise - repcol
✪✪ Given a matrix mat \(n\) x \(m\) and a lst of \(n\) elements, MODIFY mat by writing into each cell the corresponding value from lst
if
lsthas a different length from \(n\), raiseValueErrorDO NOT create new lists
Example:
>>> m = [
['z','a','p','p','a'],
['c','a','r','t','a'],
['p','a','l','l','a']
]
>>> repcol( m, ['E','H','?']) # returns nothing!
>>> m
[['E', 'E', 'E', 'E','E'],
['H', 'H', 'H', 'H','H'],
['?', '?', '?', '?','?']]
[19]:
def repcol(mat, lst):
raise Exception('TODO IMPLEMENT ME !')
m1 = [ ['a'] ]
v1 = ['Q']
repcol(m1,v1) # returns nothing
assert m1 == [['Q']]
m2 = [
['a','b'],
['c','d'],
['e','f'],
['g','h'],
]
saved = m2[0] # we save a pointer to the first original row
v2 = ['P','A','L','A']
repcol(m2,v2) # returns nothing
assert m2 == [['P', 'P'],
['A', 'A'],
['L', 'L'],
['A', 'A']]
assert id(saved) == id(m2[0]) # must not create new lists
m3 = [
['z','a','p','p','a'],
['c','a','r','t','a'],
['p','a','l','l','a']
]
v3 = ['E','H','?']
repcol(m3,v3) # returns nothing
assert m3 == [['E', 'E', 'E', 'E','E'],
['H', 'H', 'H', 'H','H'],
['?', '?', '?', '?','?']]
Exercise - matinc
✪✪ Given a matrix of integers RETURN True if all the rows are strictly increasing from left to right, otherwise return False
Example 1:
>>> m = [[1,4,6,7,9],
[0,1,2,4,8],
[2,6,8,9,10]]
>>> matinc(m)
True
Example 2:
>>> m = [[0,1,3,4],
[4,6,9,10],
[3,7,7,15]]
>>> matinc(m)
False
[20]:
def matinc(mat):
raise Exception('TODO IMPLEMENT ME !')
# TEST
m1 = [[5]]
assert matinc(m1) == True
m2 = [[7],
[4]]
assert matinc(m2) == True
m3 = [[2,3],
[3,5]]
assert matinc(m3) == True
m4 = [[9,4]]
assert matinc(m4) == False
m5 = [[5,5]]
assert matinc(m5) == False
m6 = [[1,4,6,7,9],
[0,1,2,4,8],
[2,6,8,9,10]]
assert matinc(m6) == True
m7 = [[0,1,3,4],
[4,6,9,10],
[3,7,7,15]]
assert matinc(m7) == False
m8 = [[1,4,8,7,9],
[0,1,2,4,8]]
assert matinc(m8) == False
Exercise - flip
✪✪ Takes a matrix as a list of lists containing zeros and ones, and RETURN a NEW matrix (as list of lists), built first inverting all the rows and then flipping all the rows.
Inverting a list means transform the 0 into 1 and 1 into 0 - i.e.
[0,1,1]becomes[1,0,0][0,0,1]becomes[1,1,0]
Flipping a list means flipping the elements order - i.e.
[0,1,1]becomes[1,1,0][0,0,1]becomes[1,0,0]
Example: By combining inversion and reversal, if we start from
[
[1,1,0,0],
[0,1,1,0],
[0,0,1,0]
]
First we invert each element:
[
[0,0,1,1],
[1,0,0,1],
[1,1,0,1]
]
Then we flip weach row:
[
[1,1,0,0],
[1,0,0,1],
[1,0,1,1]
]
[21]:
def flip(mat):
raise Exception('TODO IMPLEMENT ME !')
assert flip([[]]) == [[]]
assert flip([[1]]) == [[0]]
assert flip([[1,0]]) == [[1,0]]
m1 = [ [1,0,0],
[1,0,1] ]
r1 = [ [1,1,0],
[0,1,0] ]
assert flip(m1) == r1
m2 = [ [1,1,0,0],
[0,1,1,0],
[0,0,1,0] ]
r2 = [ [1,1,0,0],
[1,0,0,1],
[1,0,1,1] ]
assert flip(m2) == r2
# verify the original m was not changed!
assert m2 == [ [1,1,0,0],
[0,1,1,0],
[0,0,1,0] ]
Exercise - wall
✪✪✪ Given a list repe of repetitions and an \(n\) x \(m\) matrix mat as list of lists, RETURN a completely NEW matrix by taking the rows of mat and replicating them the number of times reported in the corresponding cells of repe
DO NOT create structures with pointers to input matrix (nor parts of it)!
Example:
>>> wall([3,4,1,2], [['i','a','a'],
['q','r','f'],
['y','e','v'],
['e','g','h']])
[['i', 'a', 'a'],
['i', 'a', 'a'],
['i', 'a', 'a'],
['q', 'r', 'f'],
['q', 'r', 'f'],
['q', 'r', 'f'],
['q', 'r', 'f'],
['y', 'e', 'v'],
['e', 'g', 'h'],
['e', 'g', 'h']]
[22]:
def wall(ripe, mat):
raise Exception('TODO IMPLEMENT ME !')
m1 = [['a']]
assert wall([2], m1) == [['a'],
['a']]
m2 = [['a','b','c','d'],
['e','q','v','r']]
r2 = wall([3,2], m2)
assert r2 == [['a','b','c','d'],
['a','b','c','d'],
['a','b','c','d'],
['e','q','v','r'],
['e','q','v','r']]
r2[0][0] = 'z'
assert m2 == [['a','b','c','d'], # we want a NEW matrix
['e','q','v','r']]
m3 = [['i','a','a'],
['q','r','f'],
['y','e','v'],
['e','g','h']]
r3 = wall([3,4,1,2], m3)
assert r3 == [['i', 'a', 'a'],
['i', 'a', 'a'],
['i', 'a', 'a'],
['q', 'r', 'f'],
['q', 'r', 'f'],
['q', 'r', 'f'],
['q', 'r', 'f'],
['y', 'e', 'v'],
['e', 'g', 'h'],
['e', 'g', 'h']]
Exercise - sortlast
✪✪✪ Given a matrix as a list of lists of integer numbers, MODIFIY the matrix by sorting ONLY the numbers of last column
All other cells must NOT change
Example:
>>> m = [[8,5,3,2,4],
[7,2,4,1,1],
[9,8,3,3,7],
[6,0,4,2,5]]
>>> sortlast(m)
>>> m
[[8, 5, 3, 2, 1],
[7, 2, 4, 1, 4],
[9, 8, 3, 3, 5],
[6, 0, 4, 2, 7]]
[23]:
def sortlast(mat):
raise Exception('TODO IMPLEMENT ME !')
# TEST
m1 = [[3]]
sortlast(m1)
assert m1 == [[3]]
m2 = [[9,3,7],
[8,5,4]]
sortlast(m2)
assert m2 == [[9,3,4],
[8,5,7]]
m3 = [[8,5,9],
[7,2,3],
[9,8,7]]
sortlast(m3)
assert m3 == [[8,5,3],
[7,2,7],
[9,8,9]]
m4 = [[8,5,3,2,4],
[7,2,4,1,1],
[9,8,3,3,7],
[6,0,4,2,5]]
sortlast(m4)
assert m4 == [[8, 5, 3, 2, 1],
[7, 2, 4, 1, 4],
[9, 8, 3, 3, 5],
[6, 0, 4, 2, 7]]
assert sortlast([[3]]) == None
Exercise - skyscraper
The profile of a city can be represented as a 2D matrix where the 1 represent the buildings. In the example below, the building height is 4 (second column from the right)
[[0, 0, 0, 0, 0, 0],
[0, 0, 0, 0, 1, 0],
[0, 0, 1, 0, 1, 0],
[0, 1, 1, 1, 1, 0],
[1, 1, 1, 1, 1, 1]]
Write a function which takes the profile of a 2-D list of 0 and 1 and RETURN the height of the highest skyscraper, for other examples see asserts
[24]:
def skyscraper(mat):
raise Exception('TODO IMPLEMENT ME !')
assert skyscraper([ [0, 0, 0, 0, 0, 0],
[0, 0, 0, 0, 1, 0],
[0, 0, 1, 0, 1, 0],
[0, 1, 1, 1, 1, 0],
[1, 1, 1, 1, 1, 1] ]) == 4
assert skyscraper([ [0, 0, 0, 0],
[0, 1, 0, 0],
[0, 1, 1, 0],
[1, 1, 1, 1] ]) == 3
assert skyscraper([ [0, 1, 0, 0],
[0, 1, 0, 0],
[0, 1, 1, 0],
[1, 1, 1, 1] ]) == 4
assert skyscraper([ [0, 0, 0, 0],
[0, 0, 0, 0],
[1, 1, 1, 0],
[1, 1, 1, 1] ]) == 2
Exercise - school lab
✪✪✪ If you’re a teacher that often see new students, you have this problem: if two students who are friends sit side by side they can start chatting way too much. To keep them quiet, you want to somehow randomize student displacement by following this algorithm:
first sort the students alphabetically
then sorted students progressively sit at the available chairs one by one, first filling the first row, then the second, till the end.
INPUT:
students: a list of strings of length <= n*m
chairs: an nxm matrix as list of lists filled with None values (empty chairs)
OUTPUT: MODIFIES BOTH students and chairs inputs, without returning anything
If students are more than available chairs, raises
ValueError
Now implement the algorithm.
Example:
ss = ['b', 'd', 'e', 'g', 'c', 'a', 'h', 'f' ]
mat = [
[None, None, None],
[None, None, None],
[None, None, None],
[None, None, None]
]
lab(ss, mat)
# after execution, mat should result changed to this:
assert mat == [
['a', 'b', 'c'],
['d', 'e', 'f'],
['g', 'h', None],
[None, None, None],
]
# after execution, input ss should now be ordered:
assert ss == ['a','b','c','d','e','f','g','f']
For more examples, see tests
Show solution[25]:
def lab(students, chairs):
raise Exception('TODO IMPLEMENT ME !')
try:
lab(['a','b'], [[None]])
raise Exception("TEST FAILED: Should have failed before with a ValueError!")
except ValueError:
"Test passed"
try:
lab(['a','b','c'], [[None,None]])
raise Exception("TEST FAILED: Should have failed before with a ValueError!")
except ValueError:
"Test passed"
m0 = [ [None] ]
r0 = lab([],m0)
assert m0 == [ [None] ]
assert r0 == None # function is not meant to return anything (so returns None by default)
m1 = [ [None] ]
r1 = lab(['a'], m1)
assert m1 == [ ['a'] ]
assert r1 == None # function is not meant to return anything (so returns None by default)
m2 = [ [None, None] ]
lab(['a'], m2) # 1 student 2 chairs in one row
assert m2 == [ ['a', None] ]
m3 = [ [None],
[None] ]
lab(['a'], m3) # 1 student 2 chairs in one column
assert m3 == [ ['a'],
[None] ]
ss4 = ['b', 'a']
m4 = [ [None, None] ]
lab(ss4, m4) # 2 students 2 chairs in one row
assert m4 == [ ['a','b'] ]
assert ss4 == ['a', 'b'] # also modified input list as required by function text
m5 = [ [None, None],
[None, None] ]
lab(['b', 'c', 'a'], m5) # 3 students 2x2 chairs
assert m5 == [ ['a','b'],
['c', None] ]
m6 = [ [None, None],
[None, None] ]
lab(['b', 'd', 'c', 'a'], m6) # 4 students 2x2 chairs
assert m6 == [ ['a','b'],
['c','d'] ]
m7 = [ [None, None, None],
[None, None, None] ]
lab(['b', 'd', 'e', 'c', 'a'], m7) # 5 students 3x2 chairs
assert m7 == [ ['a','b','c'],
['d','e',None] ]
ss8 = ['b', 'd', 'e', 'g', 'c', 'a', 'h', 'f' ]
m8 = [ [None, None, None],
[None, None, None],
[None, None, None],
[None, None, None] ]
lab(ss8, m8) # 8 students 3x4 chairs
assert m8 == [ ['a', 'b', 'c'],
['d', 'e', 'f'],
['g', 'h', None],
[None, None, None] ]
assert ss8 == ['a','b','c','d','e','f','g','h']
Exercise - dump
The multinational ToxiCorp wants to hire you for devising an automated truck driver which will deposit highly contaminated waste in the illegal dumps they own worldwide. You find it ethically questionable, but they pay well, so you accept.
A dump is modelled as a rectangular region of dimensions nrow and ncol, implemented as a list of lists matrix. Every cell i, j contains the tons of waste present, and can contain at most 7 tons of waste.
The dumpster truck will transport q tons of waste, and will try to fill the dump by depositing waste in the first row, filling each cell up to 7 tons. When the first row is filled, it will proceed to the second one from the left , then to the third one again from the left until there is no waste to dispose of.
Function dump(m, q) takes as input the dump mat and the number of tons q to dispose of, and RETURN a NEW list representing a plan with the sequence of tons to dispose.
If waste to dispose exceeds dump capacity, raises
ValueError.DO NOT modify the matrix
Example:
m = [
[5,4,6],
[4,7,1],
[3,2,6],
[3,6,2],
]
dump(m, 22)
[2, 3, 1, 3, 0, 6, 4, 3]
For first row we dispose of 2,3,1 tons in three cells, for second row we dispose of 3,0,6 tons in three cells, for third row we only dispose 4, 3 tons in two cells as limit q=22 is reached.
Show solution[26]:
def dump(mat, q):
raise Exception('TODO IMPLEMENT ME !')
m1 = [ [5] ]
assert dump(m1,0) == [] # nothing to dump
m2 = [ [4] ]
assert dump(m2,2) == [2]
m3 = [ [5,4] ]
assert dump(m3,3) == [2, 1]
m3 = [ [5,7,3] ]
assert dump(m3,3) == [2, 0, 1]
m5 = [ [2,5], # 5 2
[4,3] ] # 3 1
assert dump(m5,11) == [5,2,3,1]
# tons to dump in each cell
m6 = [ [5,4,6], # 2 3 1
[4,7,1], # 3 0 6
[3,2,6], # 4 3 0
[3,6,2] ] # 0 0 0
assert dump(m6, 22) == [2,3,1,3,0,6,4,3]
try:
dump ([[5]], 10)
raise Exception("Should have failed !")
except ValueError:
pass
Esercizio - toepliz
✪✪✪ RETURN True if the matrix as list of lists is Toeplitz, otherwise RETURN False.
A matrix is Toeplitz if and only if every diagonal contains all the same elements
We assume the matrix always contains at least a row of at least an element
HINT: use a couple of for, in the first one iterate by rows, in the second one by columns.
Ask yourself:
from which row should we start scanning? Is the first one useful?
from which column should we start scanning? Is the first one useful?
if we scan the rows from the first one toward the last one and we are examining a certain number at a certain row, which condition should that number meet for the matrix to be Toeplitz?
Examples:
>>> m1 = [
[1,2,3,4],
[5,1,2,3],
[9,5,1,2]
]
>>> toepliz(m1)
True
On every diagonal there are the same numbers so it returns True
>>> m2 = [
[1, 2, 3, 4],
[5, 1, 4, 3],
[9, 3, 1, 2]
]
>>> toepliz(m2)
False
There is at least one diagonal with different numbers, in this case we have the diagonals 5,3 and 2,4,2 so it returns False
[27]:
def toepliz(matrix):
raise Exception('TODO IMPLEMENT ME !')
# TEST START - DO NOT TOUCH !
assert toepliz([ [1] ]) == True
assert toepliz([ [3,7],
[5,3] ]) == True
assert toepliz([ [3,7],
[3,5] ]) == False
assert toepliz([ [3,7],
[3,5] ]) == False
assert toepliz([ [3,7,9],
[5,3,7] ]) == True
assert toepliz([ [3,7,9],
[5,3,8] ]) == False
assert toepliz([ [1,2,3,4],
[5,1,2,3],
[9,5,1,2] ]) == True
assert toepliz([ [1,2,3,4],
[5,9,2,3],
[9,5,1,2] ]) == False
# TEST END
Exercise - matrix multiplication
✪✪✪ Have a look at matrix multiplication definition on Wikipedia and try to implement it in the following function.
Basically, given nxm matrix A and mxp matrix B you need to output an nxp matrix C calculating the entries \(c_{ij}\) with the formula
\(c_{ij} = a_{i1}b_{1j} +\cdots + a_{im}b_{mj}= \sum_{k=1}^m a_{ik}b_{kj}\)
You need to fill all the nxp cells of C, so sure enough to fill a rectangle you need two fors. Do you also need another for ? Help yourself with the following visualization.
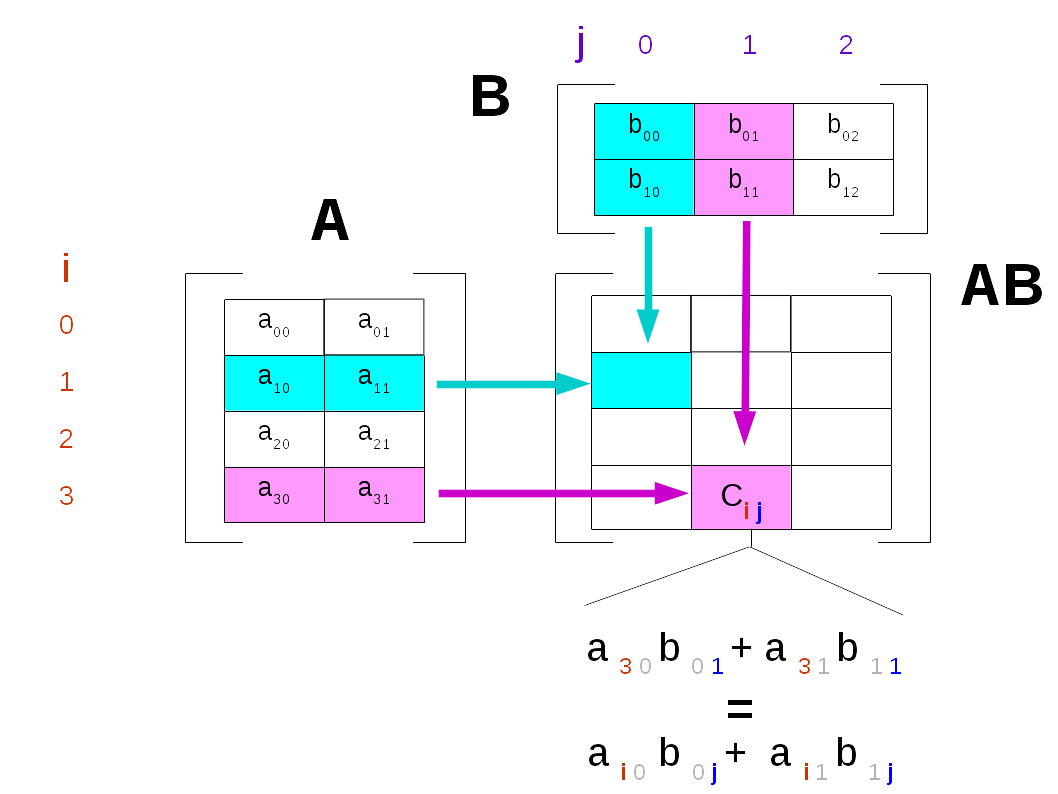
Given matrices n x m mata and m x p matb, RETURN a NEW n x p matrix which is the result of the multiplication of mata by matb.
If
matahas column number different frommatbrow number, raises aValueError.
[28]:
def mul(mata, matb):
raise Exception('TODO IMPLEMENT ME !')
# TEST START - DO NOT TOUCH!
# if you wrote the whole code correct, and execute the cell, Python shouldn't raise `AssertionError`
# let's try wrong matrix dimensions:
try:
mul([[3,5]], [[7]])
raise Exception("SHOULD HAVE FAILED!")
except ValueError:
"passed test"
ma1 = [ [3] ]
mb1 = [ [5] ]
r1 = mul(ma1,mb1)
assert r1 == [ [15] ]
ma2 = [ [3],
[5] ]
mb2 = [ [2,6] ]
r2 = mul(ma2,mb2)
assert r2 == [ [3*2, 3*6],
[5*2, 5*6] ]
ma3 = [ [3,5] ]
mb3 = [ [2],
[6] ]
r3 = mul(ma3,mb3)
assert r3 == [ [3*2 + 5*6] ]
ma4 = [ [3,5],
[7,1],
[9,4] ]
mb4 = [ [4,1,5,7],
[8,5,2,7] ]
r4 = mul(ma4,mb4)
assert r4 == [ [52, 28, 25, 56],
[36, 12, 37, 56],
[68, 29, 53, 91] ]
Exercise - check_nqueen
✪✪✪✪ A hard problem for the pros out there.
You have an \(n\) x \(n\) matrix of booleans representing a chessboard where True means there is a queen in a cell,and False there is nothing.
For the sake of visualization, we can represent a configurations using o to mean False and letters like 'A' and 'B' are queens. Contrary to what we’ve done so far, for later convenience we show the matrix with the j going from bottom to top.
Let’s see an example. In this case A and B can not attack each other, so the algorithm would return True:
7 ......B.
6 ........
5 ........
4 ........
3 ....A...
2 ........
1 ........
0 ........
i
j 01234567
Let’s see why by evidencing A attack lines ..
7 \...|.B.
6 .\..|../
5 ..\.|./.
4 ...\|/..
3 ----A---
2 .../|\..
1 ../.|.\.
0 ./..|..\
i
j 01234567
… and B attack lines:
7 ------B-
6 ...../|\
5 ..../.|.
4 .../..|.
3 ../.A.|.
2 ./....|.
1 /.....|.
0 ......|.
i
j 01234567
In this other case the algorithm would return False as A and B can attack each other:
7 \./.|...
6 -B--|--/
5 /|\.|./.
4 .|.\|/..
3 ----A---
2 .|./|\..
1 .|/.|.\.
0 ./..|..\
i
j 01234567
In your algorithm, first you need to scan for queens. When you find one (and for each one of them !), you need to check if it can hit some other queen. Let’s see how:
In this 7x7 table we have only one queen A, with at position i=1 and j=4
6 ....|..
5 \...|..
4 .\..|..
3 ..\.|./
2 ...\|/.
1 ----A--
0 .../|\.
i
j 0123456
To completely understand the range of the queen and how to calculate the diagonals, it is convenient to visually extend the table like so to have the diagonals hit the vertical axis. Notice we also added letters y and x
NOTE: in the algorithm you do not need to extend the matrix !
y
6 ....|....
5 \...|.../
4 .\..|../.
3 ..\.|./..
2 ...\|/...
1 ----A----
0 .../|\...
-1 ../.|.\..
-2 ./..|..\.
-3 /...|...\
i
j 01234567 x
We see that the top-left to bottom-right diagonal hits the vertical axis at y = 5 and the bottom-left to top-right diagonal hits the axis at y = -3. You should use this info to calculate the line equations.
Now you should have all the necessary hints to proceed with the implementation.
Show solution[29]:
def check_nqueen(mat):
""" Takes an nxn matrix of booleans representing a chessboard where True means there is a queen in a cell,
and False there is nothing. RETURN True if no queen can attack any other one, False otherwise
"""
raise Exception('TODO IMPLEMENT ME !')
assert check_nqueen([ [True] ])
assert check_nqueen([ [True, True],
[False, False] ]) == False
assert check_nqueen([ [True, False],
[False, True] ]) == False
assert check_nqueen([ [True, False],
[True, False] ]) == False
assert check_nqueen([ [True, False, False],
[False, False, True],
[False, False, False] ]) == True
assert check_nqueen([ [True, False, False],
[False, False, False],
[False, False, True] ]) == False
assert check_nqueen([ [False, True, False],
[False, False, False],
[False, False, True] ]) == True
assert check_nqueen([ [False, True, False],
[False, True, False],
[False, False, True] ]) == False
Continue
Go on with matrix challenges