Basics 2 - booleans

Download exercises zip

Browse online files

PREREQUISITES:

• Having read basics 1 integer variables

Booleans are used in boolean algebra and have the type bool.

Values of truth in Python are represented with the keywords True and False: a boolean object can only have the values True or False.

x = True

x

True

type(x)

bool

y = False

type(y)

bool

Boolean operators

We can operate on boolean values with the operators not, and, or:

and

a	b	a and b
False	False	False
False	True	False
True	False	False
True	True	True

or

a	b	a or b
False	False	False
False	True	True
True	False	True
True	True	True

not

a	not a
False	True
True	False

Questions with costants

QUESTION: For each of the following boolean expressions, try guessing the result (before guess, and then try them !):

1. not (True and False)
   

2. (not True) or (not (True or False))
   

3. not (not True)
   

4. not (True and (False or True))
   

5. not (not (not False))
   

6. True and (not (not((not False) and True)))
   

7. False or (False or ((True and True) and (True and False)))
   

Questions with variables

QUESTION: For each of these expressions, for which values of x and y they give True? Try to think an answer before trying!

NOTE: there can be many combinations that produce True, find them all

1. x or (not x)
   

2. (not x) and (not y)
   

3. x and (y or y)
   

4. x and (not y)
   

5. (not x) or  y
   

6. y or not (y and x)
   

7. x and ((not x) or not(y))
   

8. (not (not x)) and not (x and y)
   

9. x and (x or (not(x) or not(not(x or not (x)))))
   

QUESTION: For each of these expressions, for which values of x, y and z they give False?

NOTE: there can be many combinations that produce False, find them all

1. x or ((not y) or z)
   

2. x or (not y) or (not z)
   

3. not (x and y and (not z))
   

4. not (x and (not y) and (x or z))
   

5. y or ((x or y) and (not z))
   

De Morgan

There are a couple of laws that sometimes are useful:

Formula	Equivalent to
x or y	not(not x and not y)
x and y	not(not x or not y)

QUESTION: Look at following expressions, and try to rewrite them in equivalent ones by using De Morgan laws, simplifying the result wherever possible. Then verify the translation produces the same result as the original for all possible values of x and y.

1. (not x) or y
   

2. (not x) and (not y)
   

3. (not x) and (not (x or y))
   

Example:

x,y = False, False
#x,y = False, True
#x,y = True, False
#x,y = True, True

orig = x or y
trans = not((not x) and (not y))
print('orig=',orig)
print('trans=',trans)

# verify here

Conversion

We can convert booleans into intergers with the predefined function int. Each integer can be converted into a boolean (and vice versa) with bool:

bool(1)

True

bool(0)

False

bool(72)

True

bool(-5)

True

int(True)

1

int(False)

0

Each integer is valued to True except 0. Note that truth values True and False behave respectively like integers 1 and 0.

Questions - what is a boolean?

QUESTION: For each of these expressions, which results it produces?

1. bool(True)
   

2. bool(False)
   

3. bool(2 + 4)
   

4. bool(4-3-1)
   

5. int(4-3-1)
   

6. True + True
   

7. True + False
   

8. True - True
   

9. True * True
   

Evaluation order

For efficiency reasons, during the evaluation of a boolean expression if Python discovers the possible result can only be one, it then avoids to calculate further expressions. For example, in this expression:

False and x

by reading from left to right, in the moment we encounter False we already know that the result of and operation will always be False independetly from the value of x (convince yourself).

Instead, if while reading from left to right Python finds first True, it will continue the evaluation of following expressions and as result of the whole ``and`` will return the evaluation of the *last* expression_. If we are using booleans, we will not notice the differences, but by exchanging types we might get surprises:

True and 5

5

5 and True

True

False and 5

False

5 and False

False

Let’s think which order of evaluation Python might use for the or operator. Have a look at the expression:

True or x

By reading from left to right, as soon as we find the True we mich conclude that the result of the whole or must be True independently from the value of x (convince yourself).

Instead, if the first value is False, Python will continue in the evaluation until it finds a logical value True, when this happens that value will be the result of the whole expression. We can notice it if we use different costants from True and False:

False or 5

5

7 or False

7

3 or True

3

The numbers you see have always a logical result coherent with the operations we did, that is, if you see 0 the expression result is intended to have logical value False and if you see a number different from 0 the result is intended to be True (convince yourself).

QUESTION: Have a look at the following expressions, and for each of them try to guess which result it produces (or if it gives an error):

1. 0 and True
   

2. 1 and 0
   

3. True and -1
   

4. 0 and False
   

5. 0 or False
   

6. 0 or 1
   

7. False or -6
   

8. 0 or True
   

Evaluation errors

What happens if a boolean expression contains some code that would generate an error? According to intuition, the program should terminate, but it’s not always like this.

Let’s try to generate an error on purpose. During math lessons they surely told you many times that dividing a number by zero is an error because the result is not defined. So if we try to ask Python what the result of 1/0 is we will (predictably) get complaints:

print(1/0)
print('after')

---------------------------------------------------------------------------
ZeroDivisionError                         Traceback (most recent call last)
<ipython-input-51-9e1622b385b6> in <module>()
----> 1 1/0

ZeroDivisionError: division by zero

Notice that 'after' is not printed because the progam gets first interrupted.

What if we try to write like this?

False and 1/0

False

Python produces a result without complaining ! Why? Evaluating form left to right it found a False and so it concluded before hand that the expression result must be False. Many times you will not be aware of these potential problems but it is good to understand them because there are indeed situations in which you can event exploit the execution order to prevent errors (for example in if and while instructions we will see later in the book).

QUESTION: Look at the following expression, and for each of them try to guess which result it produces (or if it gives on error):

1. True and 1/0
   

2. 1/0 and 1/0
   

3. False or 1/0
   

4. True or 1/0
   

5. 1/0 or True
   

6. 1/0 or 1/0
   

7. True or (1/0 and True)
   

8. (not False) or not 1/0
   

9. True and 1/0 and True
   

10. (not True) or 1/0 or True
    

11. True and (not True) and 1/0
    

Comparison operators

Comparison operators allow to build expressions which return a boolean value:

Comparator	Description
a == b	True if and only if a = b
a != b	True if and only if a \(\neq\) b
a < b	True if and only if a < b
a > b	True if and only if a > b
a <= b	True if and only if a \(\leq\) b
a >= b	True if and only if a \(\geq\) b

3 == 3

True

3 == 5

False

a,b = 3,5

a == a

True

a == b

False

a == b - 2

True

3 != 5  # 3 is different from 5 ?

True

3 != 3  # 3 is different from 3 ?

False

3 < 5

True

5 < 5

False

5 <= 5

True

8 > 5

True

8 > 8

False

8 >= 8

True

Since the comparison are expressions which produce booleans, we can also assign the result to a variable:

x = 5 > 3

print(x)

True

Joining comparisons

Given a couple of quantities:

x, y = 7, 5

If we ask ourselves whether both x and y are greater than zero, which boolean expression should we write?

The correct way (although a bit verbose) is the following:

x > 0 and y > 0

True

WARNING: the following code instead is NOT correct:

x and y > 0    # WRONG!

Why? Apparently on some inputs it seems to work:

x,y = 7, 5
x and y > 0  # WARNING!

True

x,y = 7, -6
x and y > 0  # WARNING!

False

Does it really work on all of them?

x,y = -3, 5
x and y > 0   # WARNING!

True

Mmm we found something wrong…. What’s the reason? Implicitly, Python has considered the expression with these parenthesis:

x,y = -3,5
(x) and (y>0)  # WARNING!

True

This way it’s evident that on the left Python is considering x like it were a single boolean expression: as such, it tries to interpret the logical value of the integer -3: since it’s a number different from zero, it’s considered as True, hence the strange result.

QUESTION: What if we tried to place these parenthesis?

x,y = -3,5
(x and y) > 0   # WARNING!

Try thinking in depth all the steps Python will perform to calculate the expression.

Show answer

ANSWER: in this case both x and y are considered single boolean expressions, so Python internally will reduce the expression with these steps:

1. (True and True) > 0
   

2. True > 0
   

3. 1 > 0
   

4. True
   

Note that at step 2) True is converted to the integer value 1.

QUESTION: Look at the following expression, and for each of them try to guess which result it produces (or if it gives on error):

1. x = 3 == 4
   print(x)
   

2. x = False or True
   print(x)
   

3. True or False = x or False
   print(x)
   

4. x,y = 9,10
   z = x < y and x == 3**2
   print(z)
   

5. a,b = 7,6
   a = b
   x = a >= b + 1
   print(x)
   

6. x = 3^2
   y = 9
   print(x == y)
   

Exercise - The Lawnmower 1

Dr Angelo owns a squared lawn with a side of 100 meters, which every week is mowed by Jobe the gardener. Jobe always meticolously mowes all the field area, but one day the doctor decides to add some variety to the garden and asks Jobe to mow only some zones. Alas, Jobe is not very good in geometry and so Dr Angelo invents a sensor to detect the position, linked to a led which only lights up when the lawnmower must be turned on. Write an expression which given two coordinates x,y, produces True whnever the lawnmower is in a greenlight grass, and False in dark zones.

• Note the origin of the coordinates is in the lower left corner

• DO NOT use if commands

• WRITE a generic formula by using d (so don’t write 50…)

Show solution

d = 100

x,y = 0,  0      # False
#x,y = 25, 25    # False
#x,y = 75, 75    # False
#x,y = 75, 25    # False
#x,y = 25, 75    # True
#x,y = 100, 100  # False
#x,y = 10, 90    # True
#x,y = 60, 60    # False

# write here

x < d/2 and y > d/2

False

d = 100

x,y = 0,  0      # False
#x,y = 25, 25    # False
#x,y = 75, 75    # False
#x,y = 75, 25    # False
#x,y = 25, 75    # True
#x,y = 100, 100  # False
#x,y = 10, 90    # True
#x,y = 60, 60    # False

# write here

False

Exercise - The Lawnmower 2

Doctor Angelo now asks Jobe to mow more zones…

• DO NOT use if commands

Show solution

d = 100

x,y = 0,  0      # True
#x,y = 25, 25    # True
#x,y = 75, 75    # True
#x,y = 75, 25    # False
#x,y = 25, 75    # False
#x,y = 100, 100  # True
#x,y = 10, 90    # False
#x,y = 60, 60    # True

# write here

(x < d/2 and y < d/2) or (x > d/2 and y > d/2)

True

d = 100

x,y = 0,  0      # True
#x,y = 25, 25    # True
#x,y = 75, 75    # True
#x,y = 75, 25    # False
#x,y = 25, 75    # False
#x,y = 100, 100  # True
#x,y = 10, 90    # False
#x,y = 60, 60    # True

# write here

True

Exercise - The Lawnmower 3

Dr Angelo got tired of squared gardens, and now wants to split the garden witha a diagonal.

• DO NOT use if commands

Show solution

d = 100

x,y = 50, 10  # True
#x,y = 100,0   # True
#x,y = 75, 70  # True
#x,y = 25,75   # False
#x,y = 25, 5   # True
#x,y = 5, 80   # False
#x,y = 60, 70  # False

# write here
y < x

True

d = 100

x,y = 50, 10  # True
#x,y = 100,0   # True
#x,y = 75, 70  # True
#x,y = 25,75   # False
#x,y = 25, 5   # True
#x,y = 5, 80   # False
#x,y = 60, 70  # False

# write here

True

Exercise - The Lawnmower 4

Another day, another diagonal for Jobe..

• DO NOT use if commands

• HINT: if you don’t remember the linear equation it’s the time to look it up :-)

Show solution

d = 100

x,y = 50, 10   # True
#x,y = 0,0     # True
#x,y = 75, 70  # False
#x,y = 25,90   # False
#x,y = 25, 5   # True
#x,y = 80, 20  # False
#x,y = 25, 25  # True

# write here
y < -x + d

True

d = 100

x,y = 50, 10   # True
#x,y = 0,0     # True
#x,y = 75, 70  # False
#x,y = 25,90   # False
#x,y = 25, 5   # True
#x,y = 80, 20  # False
#x,y = 25, 25  # True

# write here

True

Exercise - The Lava Temple

During your studies you discover a map of an ancient temple, which hides marvelous treasures.

The temple measures d=80 meters each side, and is a labyrinth of corridors. You know for sure that some areas shown in red contain a fragile floor under which rivers of boiling lava are flowing: to warn about the danger while you’re walking, you build a detector which will emit a sound whenever you enter red zones.

Write a boolean expression which gives back True if you are in a danger zone, and False otherwise.

• DO NOT use if instructions

Show solution

d = 80

x,y = 0, 0     # False
#x,y = 20, 20  # False
#x,y = 60, 10  # True
#x,y = 10, 60  # True
#x,y = 20, 70  # False
#x,y = 70, 20  # False
#x,y = 70, 70  # False
#x,y = 0,60    # True
#x,y = 60,0    # True

# write here

((x > d//2) or (y > d//2)) and  (x < -y + d)

False

d = 80

x,y = 0, 0     # False
#x,y = 20, 20  # False
#x,y = 60, 10  # True
#x,y = 10, 60  # True
#x,y = 20, 70  # False
#x,y = 70, 20  # False
#x,y = 70, 70  # False
#x,y = 0,60    # True
#x,y = 60,0    # True

# write here

False

Exercise - The Tower of Gradius I

The hands of the clock on the first Gradius Tower has rotated so far of n degrees. Write some code which shows True if the hand is in the zones in evidence, False otherwise.

• DO NOT use if instructions

• n can be greater than 360

There two ways to solve the problem:

1. simple: write a long expressions with several and , or operators

2. harder: can you write a single short expression without and nor or?

Show solution

n = 20    # False
#n = 405  # False
#n = 70   # False
#n = 100  # True
#n = 460  # True
#n = 225  # True
#n = 182  # False
#n = 253  # False
#n = 275  # False
#n = 205  # False
#n = 350  # True
#n = 925  # False
#n = 815  # True
#n = 92   # True

# write here

# 1. LONG SOLUTION
# Looking at the figure, we see the zones are between 90° and 120°, 210° and 240°, 330 and 360°

# A first problem to tackle is the fact the hand can have rotated more than 360°, like 460° or 925° as in test.
# To solve this first problem, we can directly use the module operator like this
# to always get numbers between 0 and 359 included:

# m = n % 360

# This way we could simply solve the exercise with many and/or, like:

# (m >= 90 and m < 120)  or (m >= 210 and m < 240) or (m >= 330 and m < 360)     # 'long' solution

# 2. SHORT SOLUTION

# As an alternative, consider this fact: if you take sequences of 4 segments of 30° each,
# every sequence occupies 120° and we are interested to know when the hand is in the last segment,
# between 90° and 120°. We can then creatively use the modulus operator to 'shorten' the clock panel
# and ignore all the degrees after the 120th. Finally, we look whether or not m is lying in the last segment:

# m = n % 120      # number between 0 and 119 included
# m > 3 * 30

n % 120 > 90   # 'short' solution

False

n = 20    # False
#n = 405  # False
#n = 70   # False
#n = 100  # True
#n = 460  # True
#n = 225  # True
#n = 182  # False
#n = 253  # False
#n = 275  # False
#n = 205  # False
#n = 350  # True
#n = 925  # False
#n = 815  # True
#n = 92   # True

# write here

False

Exercise - The Pipe Jump

An Italian plumber is looking at 3 pipes of height t1, t2 and t3 , each having respectively 10, 20 and 30 coins above. Enthusiast, he makes a jump and reaches a height of h. Write some code which prints the number of coins taken (10,20 or 30).

• DO NOT use if instructions

• HINT: If you don’t know how to do it, check again the paragraph Evaluation order and try thinking how to produce numbers when only a certain condition is true …

Show solution

t1,t2,t3 = 200,500,600

h=450   # 10
#h=570  # 20
#h=610  # 30
#h=50   # 0

# write here

(h >= t3 and 30) or (h >= t2 and 20) or (h >= t1 and 10) or 0

10

t1,t2,t3 = 200,500,600

h=450   # 10
#h=570  # 20
#h=610  # 30
#h=50   # 0

# write here

10

Exercise - The Tower of Gradius II

The hands of the clock on the second Gradius Tower have rotated so far of n and m degrees. Write some code which shows True if both hands are in the same zone among the highlighted ones, False otherwise.

• DO NOT use if instructions

• n and m can be greater than 360

Show solution

n,m = 160,170   # True
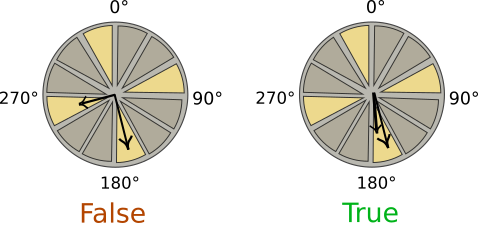
#n,m = 135, 140 # False
#n,m = 160,190  # False
#n,m = 70,170   # False
#n,m = 350,260  # False
#n,m = 350,340  # True
#n,m = 350,340  # True
#n,m = 430,530  # False
#n,m = 520,510  # True
#n,m = 730,740  # False

# write here
(n % 90 > 60) and ((n // 90) % 4 == (m // 90) % 4)

True

n,m = 160,170   # True
#n,m = 135, 140 # False
#n,m = 160,190  # False
#n,m = 70,170   # False
#n,m = 350,260  # False
#n,m = 350,340  # True
#n,m = 350,340  # True
#n,m = 430,530  # False
#n,m = 520,510  # True
#n,m = 730,740  # False

# write here

True

Continue

Go on with Basics 3 - float numbers